Super-Resolution without High-Resolution Labels for Black Hole Simulations

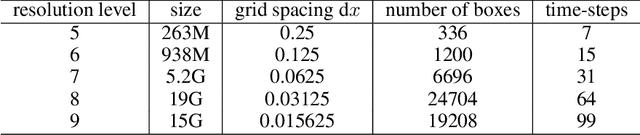
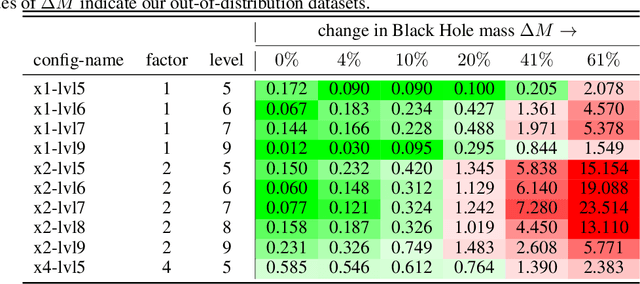
Generating high-resolution simulations is key for advancing our understanding of one of the universe's most violent events: Black Hole mergers. However, generating Black Hole simulations is limited by prohibitive computational costs and scalability issues, reducing the simulation's fidelity and resolution achievable within reasonable time frames and resources. In this work, we introduce a novel method that circumvents these limitations by applying a super-resolution technique without directly needing high-resolution labels, leveraging the Hamiltonian and momentum constraints-fundamental equations in general relativity that govern the dynamics of spacetime. We demonstrate that our method achieves a reduction in constraint violation by one to two orders of magnitude and generalizes effectively to out-of-distribution simulations.

GeometricImageNet: Extending convolutional neural networks to vector and tensor images

Convolutional neural networks and their ilk have been very successful for many learning tasks involving images. These methods assume that the input is a scalar image representing the intensity in each pixel, possibly in multiple channels for color images. In natural-science domains however, image-like data sets might have vectors (velocity, say), tensors (polarization, say), pseudovectors (magnetic field, say), or other geometric objects in each pixel. Treating the components of these objects as independent channels in a CNN neglects their structure entirely. Our formulation -- the GeometricImageNet -- combines a geometric generalization of convolution with outer products, tensor index contractions, and tensor index permutations to construct geometric-image functions of geometric images that use and benefit from the tensor structure. The framework permits, with a very simple adjustment, restriction to function spaces that are exactly equivariant to translations, discrete rotations, and reflections. We use representation theory to quantify the dimension of the space of equivariant polynomial functions on 2-dimensional vector images. We give partial results on the expressivity of GeometricImageNet on small images. In numerical experiments, we find that GeometricImageNet has good generalization for a small simulated physics system, even when trained with a small training set. We expect this tool will be valuable for scientific and engineering machine learning, for example in cosmology or ocean dynamics.

The CAMELS project: public data release

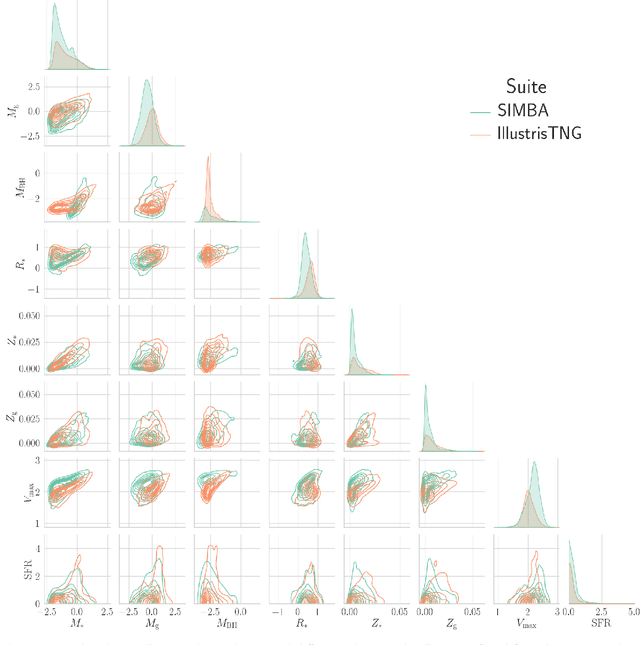
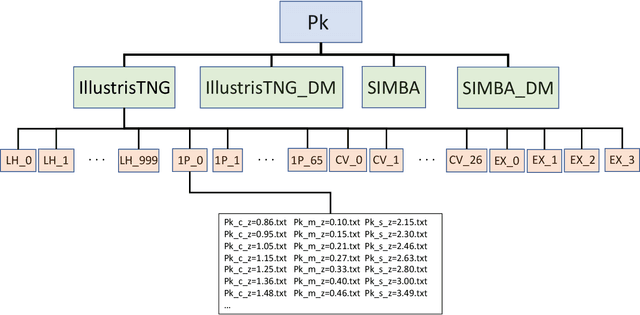
The Cosmology and Astrophysics with MachinE Learning Simulations (CAMELS) project was developed to combine cosmology with astrophysics through thousands of cosmological hydrodynamic simulations and machine learning. CAMELS contains 4,233 cosmological simulations, 2,049 N-body and 2,184 state-of-the-art hydrodynamic simulations that sample a vast volume in parameter space. In this paper we present the CAMELS public data release, describing the characteristics of the CAMELS simulations and a variety of data products generated from them, including halo, subhalo, galaxy, and void catalogues, power spectra, bispectra, Lyman-$\alpha$ spectra, probability distribution functions, halo radial profiles, and X-rays photon lists. We also release over one thousand catalogues that contain billions of galaxies from CAMELS-SAM: a large collection of N-body simulations that have been combined with the Santa Cruz Semi-Analytic Model. We release all the data, comprising more than 350 terabytes and containing 143,922 snapshots, millions of halos, galaxies and summary statistics. We provide further technical details on how to access, download, read, and process the data at \url{https://camels.readthedocs.io}.

The CAMELS Multifield Dataset: Learning the Universe's Fundamental Parameters with Artificial Intelligence

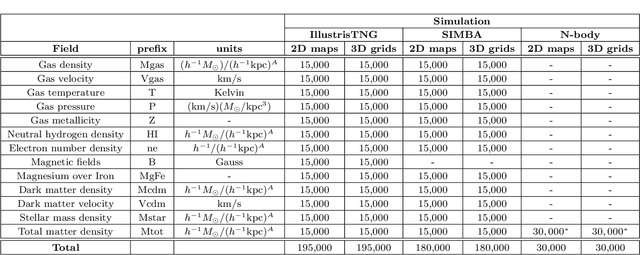
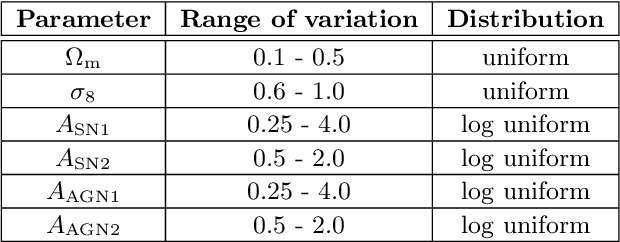
We present the Cosmology and Astrophysics with MachinE Learning Simulations (CAMELS) Multifield Dataset, CMD, a collection of hundreds of thousands of 2D maps and 3D grids containing many different properties of cosmic gas, dark matter, and stars from 2,000 distinct simulated universes at several cosmic times. The 2D maps and 3D grids represent cosmic regions that span $\sim$100 million light years and have been generated from thousands of state-of-the-art hydrodynamic and gravity-only N-body simulations from the CAMELS project. Designed to train machine learning models, CMD is the largest dataset of its kind containing more than 70 Terabytes of data. In this paper we describe CMD in detail and outline a few of its applications. We focus our attention on one such task, parameter inference, formulating the problems we face as a challenge to the community. We release all data and provide further technical details at https://camels-multifield-dataset.readthedocs.io.