Super-Resolution without High-Resolution Labels for Black Hole Simulations

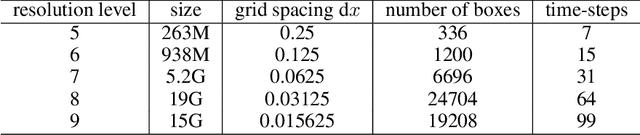
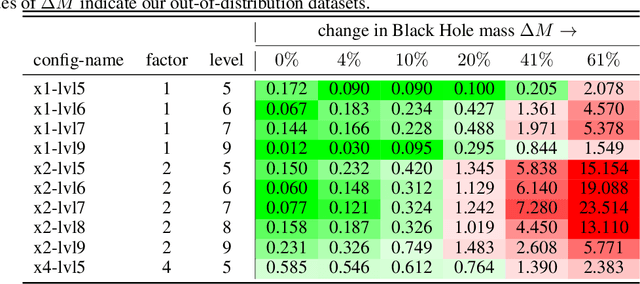
Generating high-resolution simulations is key for advancing our understanding of one of the universe's most violent events: Black Hole mergers. However, generating Black Hole simulations is limited by prohibitive computational costs and scalability issues, reducing the simulation's fidelity and resolution achievable within reasonable time frames and resources. In this work, we introduce a novel method that circumvents these limitations by applying a super-resolution technique without directly needing high-resolution labels, leveraging the Hamiltonian and momentum constraints-fundamental equations in general relativity that govern the dynamics of spacetime. We demonstrate that our method achieves a reduction in constraint violation by one to two orders of magnitude and generalizes effectively to out-of-distribution simulations.

Scaling-laws for Large Time-series Models

Scaling laws for large language models (LLMs) have provided useful guidance on how to train ever larger models for predictable performance gains. Time series forecasting shares a similar sequential structure to language, and is amenable to large-scale transformer architectures. Here we show that foundational decoder-only time series transformer models exhibit analogous scaling-behavior to LLMs, while architectural details (aspect ratio and number of heads) have a minimal effect over broad ranges. We assemble a large corpus of heterogenous time series data on which to train, and establish, for the first time, power-law scaling relations with respect to parameter count, dataset size, and training compute, spanning five orders of magnitude.

Optimal simulation-based Bayesian decisions

We present a framework for the efficient computation of optimal Bayesian decisions under intractable likelihoods, by learning a surrogate model for the expected utility (or its distribution) as a function of the action and data spaces. We leverage recent advances in simulation-based inference and Bayesian optimization to develop active learning schemes to choose where in parameter and action spaces to simulate. This allows us to learn the optimal action in as few simulations as possible. The resulting framework is extremely simulation efficient, typically requiring fewer model calls than the associated posterior inference task alone, and a factor of $100-1000$ more efficient than Monte-Carlo based methods. Our framework opens up new capabilities for performing Bayesian decision making, particularly in the previously challenging regime where likelihoods are intractable, and simulations expensive.