FLUID-LLM: Learning Computational Fluid Dynamics with Spatiotemporal-aware Large Language Models

Learning computational fluid dynamics (CFD) traditionally relies on computationally intensive simulations of the Navier-Stokes equations. Recently, large language models (LLMs) have shown remarkable pattern recognition and reasoning abilities in natural language processing (NLP) and computer vision (CV). However, these models struggle with the complex geometries inherent in fluid dynamics. We introduce FLUID-LLM, a novel framework combining pre-trained LLMs with spatiotemporal-aware encoding to predict unsteady fluid dynamics. Our approach leverages the temporal autoregressive abilities of LLMs alongside spatial-aware layers, bridging the gap between previous CFD prediction methods. Evaluations on standard benchmarks reveal significant performance improvements across various fluid datasets. Our results demonstrate that FLUID-LLM effectively integrates spatiotemporal information into pre-trained LLMs, enhancing CFD task performance.

Incorporating LLM Priors into Tabular Learners

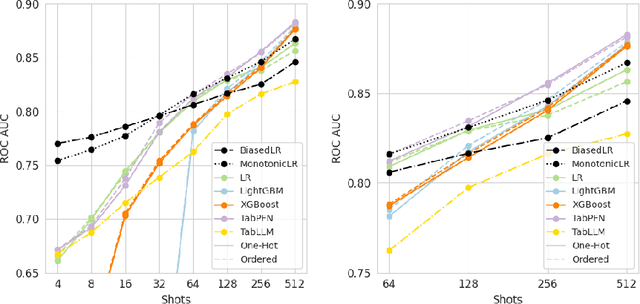
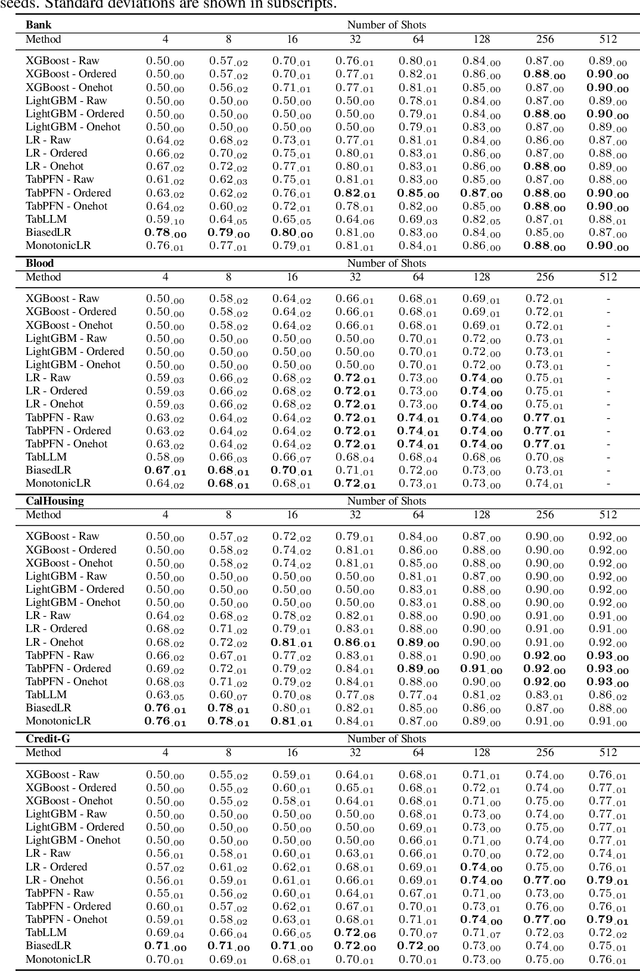
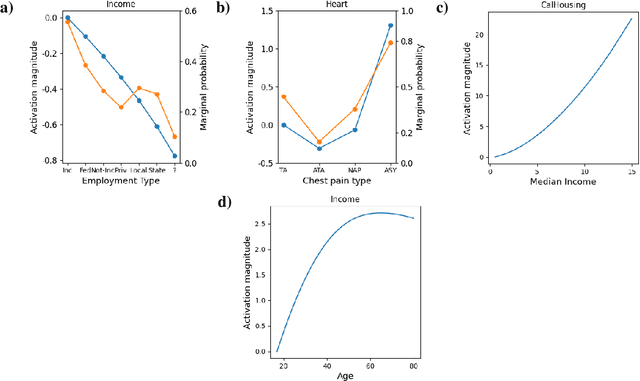
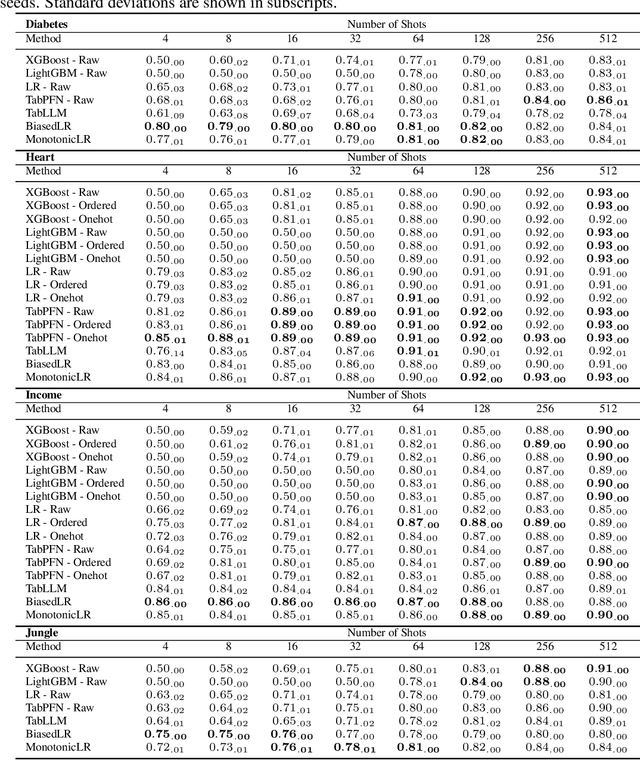
We present a method to integrate Large Language Models (LLMs) and traditional tabular data classification techniques, addressing LLMs challenges like data serialization sensitivity and biases. We introduce two strategies utilizing LLMs for ranking categorical variables and generating priors on correlations between continuous variables and targets, enhancing performance in few-shot scenarios. We focus on Logistic Regression, introducing MonotonicLR that employs a non-linear monotonic function for mapping ordinals to cardinals while preserving LLM-determined orders. Validation against baseline models reveals the superior performance of our approach, especially in low-data scenarios, while remaining interpretable.

Tabular Few-Shot Generalization Across Heterogeneous Feature Spaces

Despite the prevalence of tabular datasets, few-shot learning remains under-explored within this domain. Existing few-shot methods are not directly applicable to tabular datasets due to varying column relationships, meanings, and permutational invariance. To address these challenges, we propose FLAT-a novel approach to tabular few-shot learning, encompassing knowledge sharing between datasets with heterogeneous feature spaces. Utilizing an encoder inspired by Dataset2Vec, FLAT learns low-dimensional embeddings of datasets and their individual columns, which facilitate knowledge transfer and generalization to previously unseen datasets. A decoder network parametrizes the predictive target network, implemented as a Graph Attention Network, to accommodate the heterogeneous nature of tabular datasets. Experiments on a diverse collection of 118 UCI datasets demonstrate FLAT's successful generalization to new tabular datasets and a considerable improvement over the baselines.

Modular Neural Ordinary Differential Equations

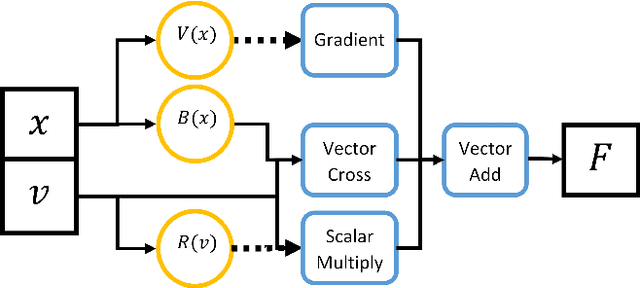
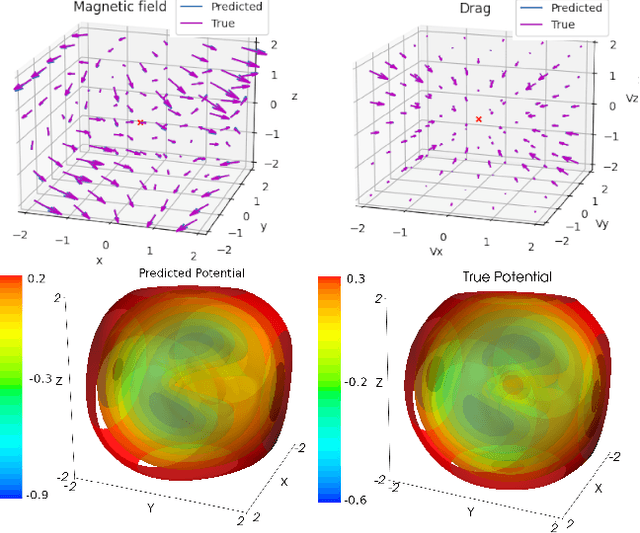
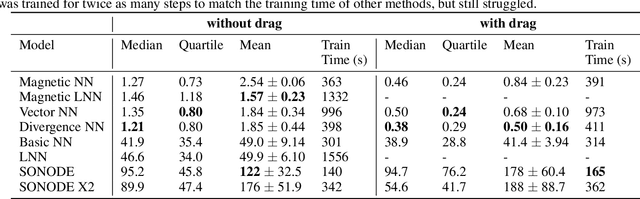
The laws of physics have been written in the language of dif-ferential equations for centuries. Neural Ordinary Differen-tial Equations (NODEs) are a new machine learning architecture which allows these differential equations to be learned from a dataset. These have been applied to classical dynamics simulations in the form of Lagrangian Neural Net-works (LNNs) and Second Order Neural Differential Equations (SONODEs). However, they either cannot represent the most general equations of motion or lack interpretability. In this paper, we propose Modular Neural ODEs, where each force component is learned with separate modules. We show how physical priors can be easily incorporated into these models. Through a number of experiments, we demonstrate these result in better performance, are more interpretable, and add flexibility due to their modularity.