Fourier Neural Differential Equations for learning Quantum Field Theories

A Quantum Field Theory is defined by its interaction Hamiltonian, and linked to experimental data by the scattering matrix. The scattering matrix is calculated as a perturbative series, and represented succinctly as a first order differential equation in time. Neural Differential Equations (NDEs) learn the time derivative of a residual network's hidden state, and have proven efficacy in learning differential equations with physical constraints. Hence using an NDE to learn particle scattering matrices presents a possible experiment-theory phenomenological connection. In this paper, NDE models are used to learn $\phi^4$ theory, Scalar-Yukawa theory and Scalar Quantum Electrodynamics. A new NDE architecture is also introduced, the Fourier Neural Differential Equation (FNDE), which combines NDE integration and Fourier network convolution. The FNDE model demonstrates better generalisability than the non-integrated equivalent FNO model. It is also shown that by training on scattering data, the interaction Hamiltonian of a theory can be extracted from network parameters.

Faster Training of Neural ODEs Using Gauß-Legendre Quadrature

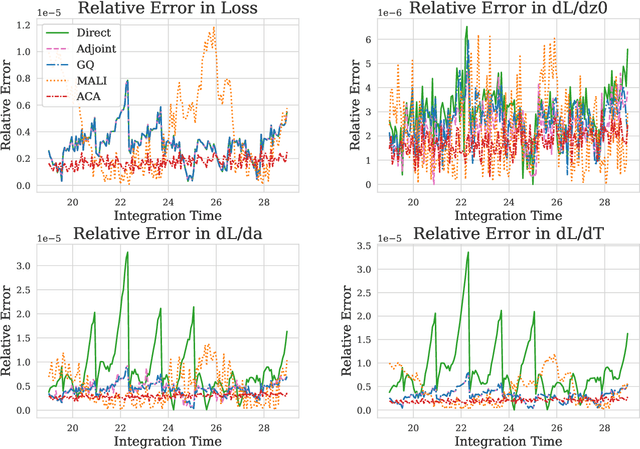
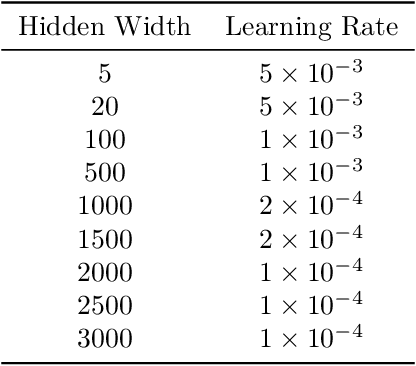
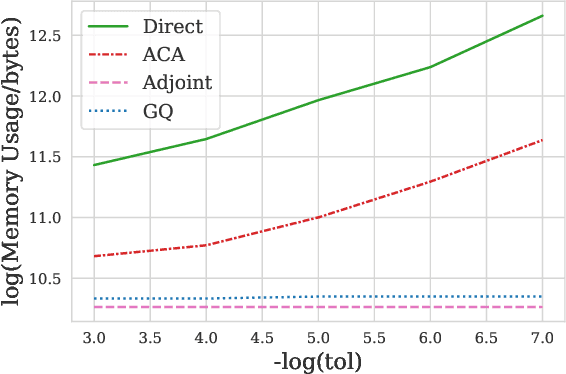
Neural ODEs demonstrate strong performance in generative and time-series modelling. However, training them via the adjoint method is slow compared to discrete models due to the requirement of numerically solving ODEs. To speed neural ODEs up, a common approach is to regularise the solutions. However, this approach may affect the expressivity of the model; when the trajectory itself matters, this is particularly important. In this paper, we propose an alternative way to speed up the training of neural ODEs. The key idea is to speed up the adjoint method by using Gau{\ss}-Legendre quadrature to solve integrals faster than ODE-based methods while remaining memory efficient. We also extend the idea to training SDEs using the Wong-Zakai theorem, by training a corresponding ODE and transferring the parameters. Our approach leads to faster training of neural ODEs, especially for large models. It also presents a new way to train SDE-based models.

SurvivalGAN: Generating Time-to-Event Data for Survival Analysis

Synthetic data is becoming an increasingly promising technology, and successful applications can improve privacy, fairness, and data democratization. While there are many methods for generating synthetic tabular data, the task remains non-trivial and unexplored for specific scenarios. One such scenario is survival data. Here, the key difficulty is censoring: for some instances, we are not aware of the time of event, or if one even occurred. Imbalances in censoring and time horizons cause generative models to experience three new failure modes specific to survival analysis: (1) generating too few at-risk members; (2) generating too many at-risk members; and (3) censoring too early. We formalize these failure modes and provide three new generative metrics to quantify them. Following this, we propose SurvivalGAN, a generative model that handles survival data firstly by addressing the imbalance in the censoring and event horizons, and secondly by using a dedicated mechanism for approximating time-to-event/censoring. We evaluate this method via extensive experiments on medical datasets. SurvivalGAN outperforms multiple baselines at generating survival data, and in particular addresses the failure modes as measured by the new metrics, in addition to improving downstream performance of survival models trained on the synthetic data.

Longitudinal Modeling of Multiple Sclerosis using Continuous Time Models

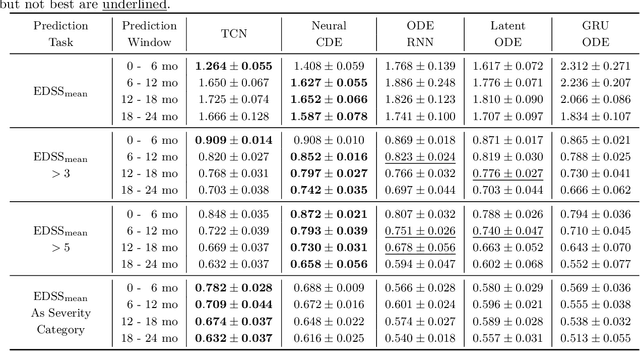
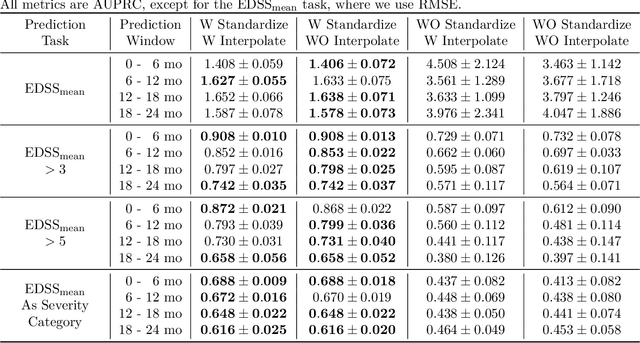
Multiple sclerosis is a disease that affects the brain and spinal cord, it can lead to severe disability and has no known cure. The majority of prior work in machine learning for multiple sclerosis has been centered around using Magnetic Resonance Imaging scans or laboratory tests; these modalities are both expensive to acquire and can be unreliable. In a recent paper it was shown that disease progression can be predicted effectively using performance outcome measures (POMs) and demographic data. In our work we extend on this to focus on the modeling side, using continuous time models on POMs and demographic data to predict progression. We evaluate four continuous time models using a publicly available multiple sclerosis dataset. We find that continuous models are often able to outperform discrete time models. We also carry out an extensive ablation to discover the sources of performance gains, we find that standardizing existing features leads to a larger performance increase than interpolating missing features.

Learning Feynman Diagrams using Graph Neural Networks

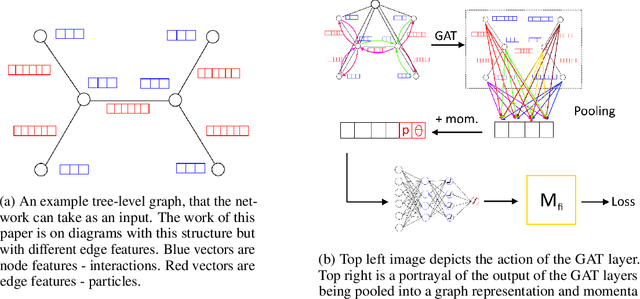
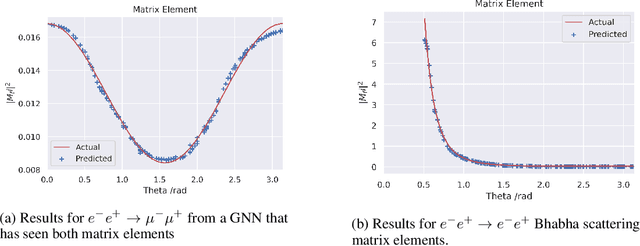
In the wake of the growing popularity of machine learning in particle physics, this work finds a new application of geometric deep learning on Feynman diagrams to make accurate and fast matrix element predictions with the potential to be used in analysis of quantum field theory. This research uses the graph attention layer which makes matrix element predictions to 1 significant figure accuracy above 90% of the time. Peak performance was achieved in making predictions to 3 significant figure accuracy over 10% of the time with less than 200 epochs of training, serving as a proof of concept on which future works can build upon for better performance. Finally, a procedure is suggested, to use the network to make advancements in quantum field theory by constructing Feynman diagrams with effective particles that represent non-perturbative calculations.

Composite Feature Selection using Deep Ensembles

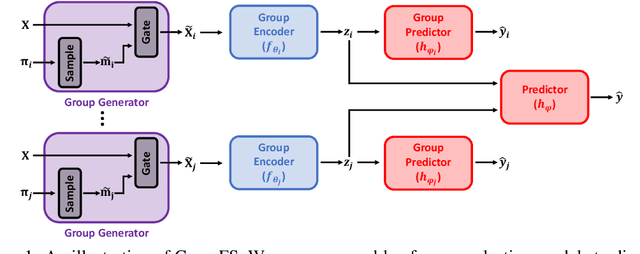
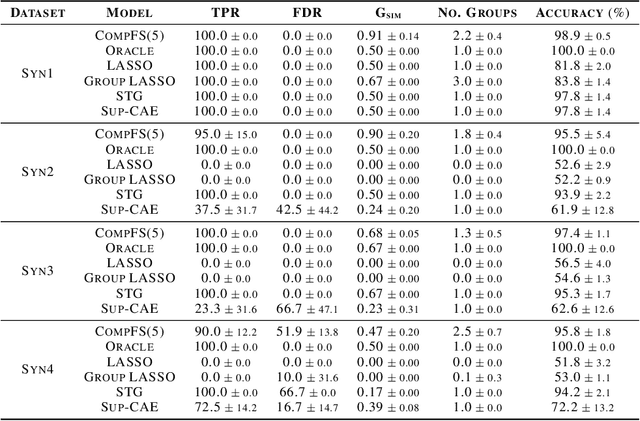
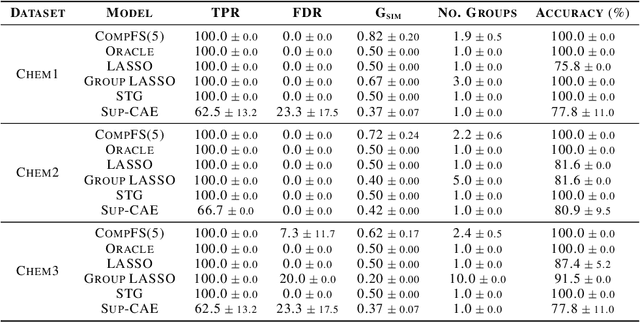
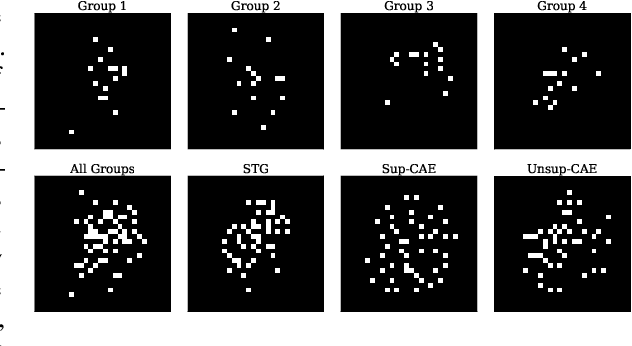
In many real world problems, features do not act alone but in combination with each other. For example, in genomics, diseases might not be caused by any single mutation but require the presence of multiple mutations. Prior work on feature selection either seeks to identify individual features or can only determine relevant groups from a predefined set. We investigate the problem of discovering groups of predictive features without predefined grouping. To do so, we define predictive groups in terms of linear and non-linear interactions between features. We introduce a novel deep learning architecture that uses an ensemble of feature selection models to find predictive groups, without requiring candidate groups to be provided. The selected groups are sparse and exhibit minimum overlap. Furthermore, we propose a new metric to measure similarity between discovered groups and the ground truth. We demonstrate the utility of our model on multiple synthetic tasks and semi-synthetic chemistry datasets, where the ground truth structure is known, as well as an image dataset and a real-world cancer dataset.

Meta-learning using privileged information for dynamics

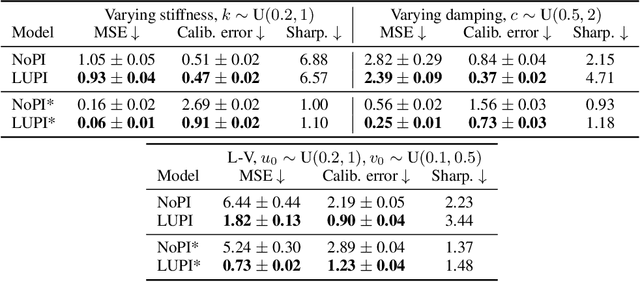
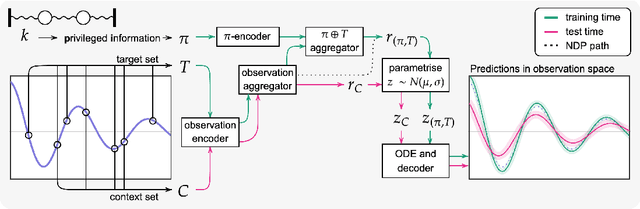
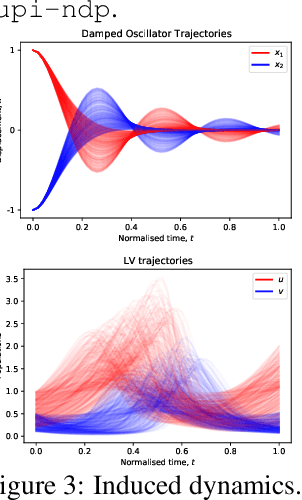
Neural ODE Processes approach the problem of meta-learning for dynamics using a latent variable model, which permits a flexible aggregation of contextual information. This flexibility is inherited from the Neural Process framework and allows the model to aggregate sets of context observations of arbitrary size into a fixed-length representation. In the physical sciences, we often have access to structured knowledge in addition to raw observations of a system, such as the value of a conserved quantity or a description of an understood component. Taking advantage of the aggregation flexibility, we extend the Neural ODE Process model to use additional information within the Learning Using Privileged Information setting, and we validate our extension with experiments showing improved accuracy and calibration on simulated dynamics tasks.

Neural ODE Processes

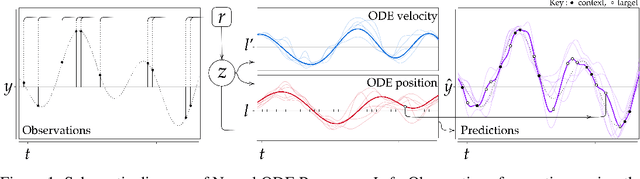
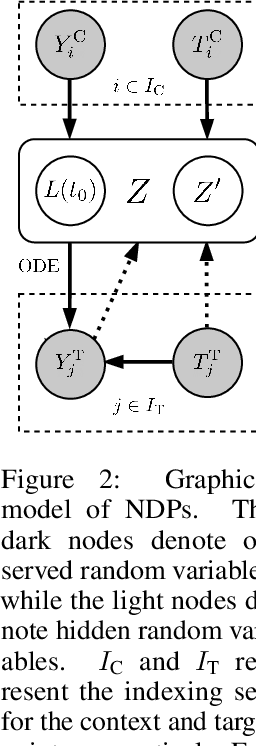
Neural Ordinary Differential Equations (NODEs) use a neural network to model the instantaneous rate of change in the state of a system. However, despite their apparent suitability for dynamics-governed time-series, NODEs present a few disadvantages. First, they are unable to adapt to incoming data-points, a fundamental requirement for real-time applications imposed by the natural direction of time. Second, time-series are often composed of a sparse set of measurements that could be explained by many possible underlying dynamics. NODEs do not capture this uncertainty. In contrast, Neural Processes (NPs) are a family of models providing uncertainty estimation and fast data-adaptation, but lack an explicit treatment of the flow of time. To address these problems, we introduce Neural ODE Processes (NDPs), a new class of stochastic processes determined by a distribution over Neural ODEs. By maintaining an adaptive data-dependent distribution over the underlying ODE, we show that our model can successfully capture the dynamics of low-dimensional systems from just a few data-points. At the same time, we demonstrate that NDPs scale up to challenging high-dimensional time-series with unknown latent dynamics such as rotating MNIST digits.

On Second Order Behaviour in Augmented Neural ODEs

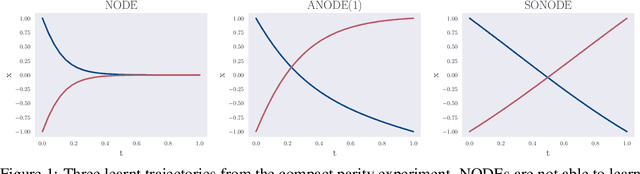
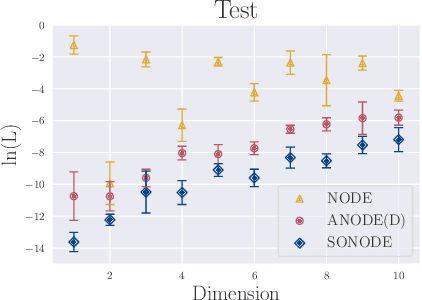
Neural Ordinary Differential Equations (NODEs) are a new class of models that transform data continuously through infinite-depth architectures. The continuous nature of NODEs has made them particularly suitable for learning the dynamics of complex physical systems. While previous work has mostly been focused on first order ODEs, the dynamics of many systems, especially in classical physics, are governed by second order laws. In this work, we take a closer look at Second Order Neural ODEs (SONODEs). We show how the adjoint sensitivity method can be extended to SONODEs and prove that an alternative first order optimisation method is computationally more efficient. Furthermore, we extend the theoretical understanding of the broader class of Augmented NODEs (ANODEs) by showing they can also learn higher order dynamics, but at the cost of interpretability. This indicates that the advantages of ANODEs go beyond the extra space offered by the augmented dimensions, as originally thought. Finally, we compare SONODEs and ANODEs on synthetic and real dynamical systems and demonstrate that the inductive biases of the former generally result in faster training and better performance.