Jake Topping
Understanding over-squashing and bottlenecks on graphs via curvature
Nov 29, 2021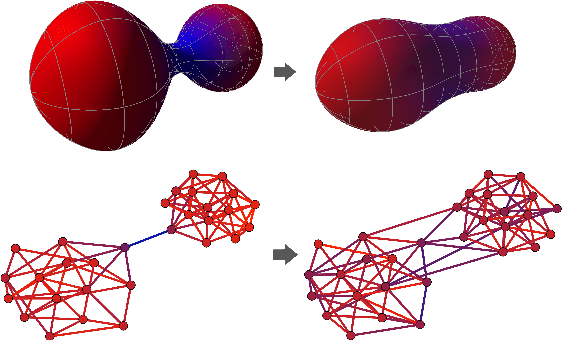
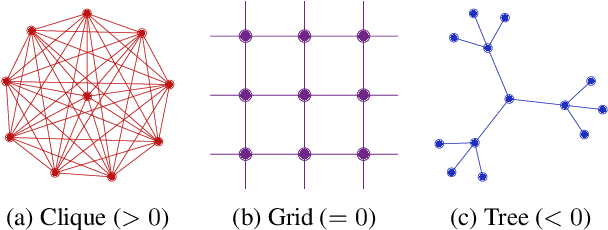


Abstract:Most graph neural networks (GNNs) use the message passing paradigm, in which node features are propagated on the input graph. Recent works pointed to the distortion of information flowing from distant nodes as a factor limiting the efficiency of message passing for tasks relying on long-distance interactions. This phenomenon, referred to as 'over-squashing', has been heuristically attributed to graph bottlenecks where the number of $k$-hop neighbors grows rapidly with $k$. We provide a precise description of the over-squashing phenomenon in GNNs and analyze how it arises from bottlenecks in the graph. For this purpose, we introduce a new edge-based combinatorial curvature and prove that negatively curved edges are responsible for the over-squashing issue. We also propose and experimentally test a curvature-based graph rewiring method to alleviate the over-squashing.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge