AWP: Activation-Aware Weight Pruning and Quantization with Projected Gradient Descent

To address the enormous size of Large Language Models (LLMs), model compression methods, such as quantization and pruning, are often deployed, especially on edge devices. In this work, we focus on layer-wise post-training quantization and pruning. Drawing connections between activation-aware weight pruning and sparse approximation problems, and motivated by the success of Iterative Hard Thresholding (IHT), we propose a unified method for Activation-aware Weight pruning and quantization via Projected gradient descent (AWP). Our experiments demonstrate that AWP outperforms state-of-the-art LLM pruning and quantization methods. Theoretical convergence guarantees of the proposed method for pruning are also provided.

TuneComp: Joint Fine-tuning and Compression for Large Foundation Models

To reduce model size during post-training, compression methods, including knowledge distillation, low-rank approximation, and pruning, are often applied after fine-tuning the model. However, sequential fine-tuning and compression sacrifices performance, while creating a larger than necessary model as an intermediate step. In this work, we aim to reduce this gap, by directly constructing a smaller model while guided by the downstream task. We propose to jointly fine-tune and compress the model by gradually distilling it to a pruned low-rank structure. Experiments demonstrate that joint fine-tuning and compression significantly outperforms other sequential compression methods.

LatentLLM: Attention-Aware Joint Tensor Compression

Modern foundation models such as large language models (LLMs) and large multi-modal models (LMMs) require a massive amount of computational and memory resources. We propose a new framework to convert such LLMs/LMMs into a reduced-dimension latent structure. Our method extends a local activation-aware tensor decomposition to a global attention-aware joint tensor de-composition. Our framework can significantly improve the model accuracy over the existing model compression methods when reducing the latent dimension to realize computationally/memory-efficient LLMs/LLMs. We show the benefit on several benchmark including multi-modal reasoning tasks.

SuperLoRA: Parameter-Efficient Unified Adaptation of Multi-Layer Attention Modules

Low-rank adaptation (LoRA) and its variants are widely employed in fine-tuning large models, including large language models for natural language processing and diffusion models for computer vision. This paper proposes a generalized framework called SuperLoRA that unifies and extends different LoRA variants, which can be realized under different hyper-parameter settings. Introducing grouping, folding, shuffling, projecting, and tensor factoring, SuperLoRA offers high flexibility compared with other LoRA variants and demonstrates superior performance for transfer learning tasks especially in the extremely few-parameter regimes.

G-RepsNet: A Fast and General Construction of Equivariant Networks for Arbitrary Matrix Groups

Group equivariance is a strong inductive bias useful in a wide range of deep learning tasks. However, constructing efficient equivariant networks for general groups and domains is difficult. Recent work by Finzi et al. (2021) directly solves the equivariance constraint for arbitrary matrix groups to obtain equivariant MLPs (EMLPs). But this method does not scale well and scaling is crucial in deep learning. Here, we introduce Group Representation Networks (G-RepsNets), a lightweight equivariant network for arbitrary matrix groups with features represented using tensor polynomials. The key intuition for our design is that using tensor representations in the hidden layers of a neural network along with simple inexpensive tensor operations can lead to expressive universal equivariant networks. We find G-RepsNet to be competitive to EMLP on several tasks with group symmetries such as O(5), O(1, 3), and O(3) with scalars, vectors, and second-order tensors as data types. On image classification tasks, we find that G-RepsNet using second-order representations is competitive and often even outperforms sophisticated state-of-the-art equivariant models such as GCNNs (Cohen & Welling, 2016a) and E(2)-CNNs (Weiler & Cesa, 2019). To further illustrate the generality of our approach, we show that G-RepsNet is competitive to G-FNO (Helwig et al., 2023) and EGNN (Satorras et al., 2021) on N-body predictions and solving PDEs, respectively, while being efficient.

Convergent Block Coordinate Descent for Training Tikhonov Regularized Deep Neural Networks

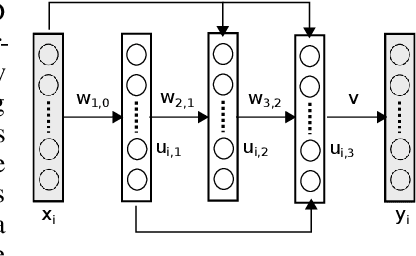
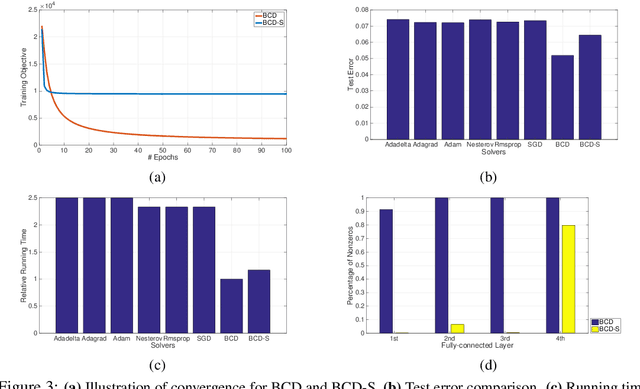
By lifting the ReLU function into a higher dimensional space, we develop a smooth multi-convex formulation for training feed-forward deep neural networks (DNNs). This allows us to develop a block coordinate descent (BCD) training algorithm consisting of a sequence of numerically well-behaved convex optimizations. Using ideas from proximal point methods in convex analysis, we prove that this BCD algorithm will converge globally to a stationary point with R-linear convergence rate of order one. In experiments with the MNIST database, DNNs trained with this BCD algorithm consistently yielded better test-set error rates than identical DNN architectures trained via all the stochastic gradient descent (SGD) variants in the Caffe toolbox.

Marginalizing Out Future Passengers in Group Elevator Control

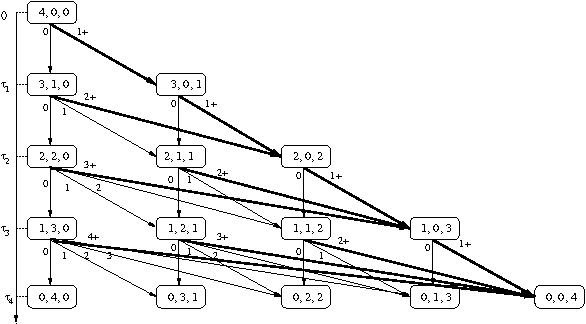
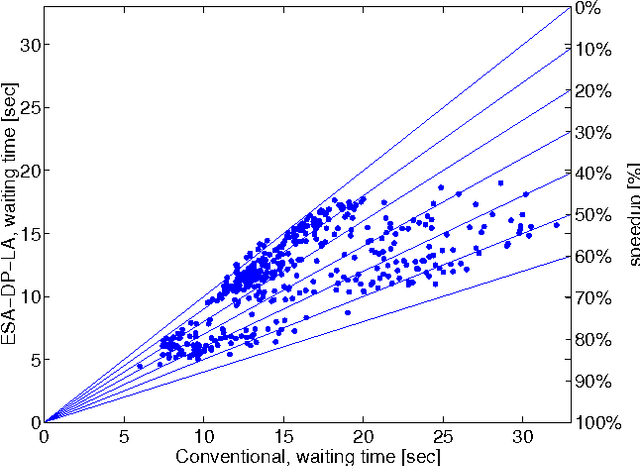
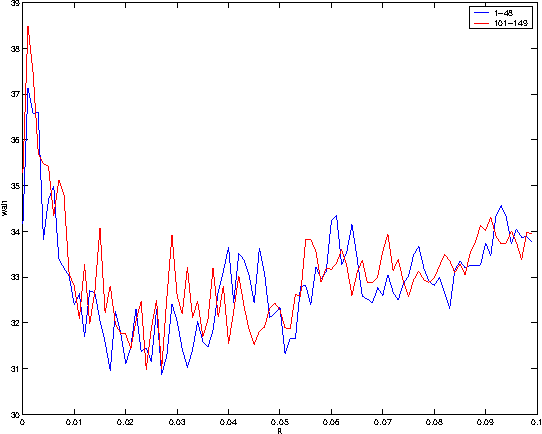
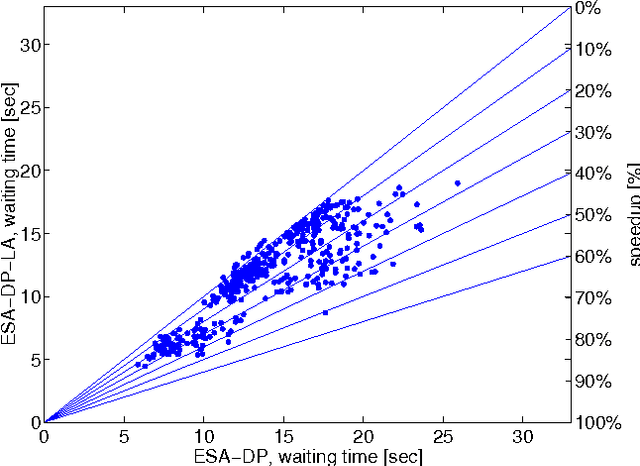
Group elevator scheduling is an NP-hard sequential decision-making problem with unbounded state spaces and substantial uncertainty. Decision-theoretic reasoning plays a surprisingly limited role in fielded systems. A new opportunity for probabilistic methods has opened with the recent discovery of a tractable solution for the expected waiting times of all passengers in the building, marginalized over all possible passenger itineraries. Though commercially competitive, this solution does not contemplate future passengers. Yet in up-peak traffic, the effects of future passengers arriving at the lobby and entering elevator cars can dominate all waiting times. We develop a probabilistic model of how these arrivals affect the behavior of elevator cars at the lobby, and demonstrate how this model can be used to very significantly reduce the average waiting time of all passengers.