Indoor Airflow Imaging Using Physics-Informed Background-Oriented Schlieren Tomography

We develop a framework for non-invasive volumetric indoor airflow estimation from a single viewpoint using background-oriented schlieren (BOS) measurements and physics-informed reconstruction. Our framework utilizes a light projector that projects a pattern onto a target back-wall and a camera that observes small distortions in the light pattern. While the single-view BOS tomography problem is severely ill-posed, our proposed framework addresses this using: (1) improved ray tracing, (2) a physics-based light rendering approach and loss formulation, and (3) a physics-based regularization using a physics-informed neural network (PINN) to ensure that the reconstructed airflow is consistent with the governing equations for buoyancy-driven flows.

AWP: Activation-Aware Weight Pruning and Quantization with Projected Gradient Descent

To address the enormous size of Large Language Models (LLMs), model compression methods, such as quantization and pruning, are often deployed, especially on edge devices. In this work, we focus on layer-wise post-training quantization and pruning. Drawing connections between activation-aware weight pruning and sparse approximation problems, and motivated by the success of Iterative Hard Thresholding (IHT), we propose a unified method for Activation-aware Weight pruning and quantization via Projected gradient descent (AWP). Our experiments demonstrate that AWP outperforms state-of-the-art LLM pruning and quantization methods. Theoretical convergence guarantees of the proposed method for pruning are also provided.

Time-Series U-Net with Recurrence for Noise-Robust Imaging Photoplethysmography

Remote estimation of vital signs enables health monitoring for situations in which contact-based devices are either not available, too intrusive, or too expensive. In this paper, we present a modular, interpretable pipeline for pulse signal estimation from video of the face that achieves state-of-the-art results on publicly available datasets.Our imaging photoplethysmography (iPPG) system consists of three modules: face and landmark detection, time-series extraction, and pulse signal/pulse rate estimation. Unlike many deep learning methods that make use of a single black-box model that maps directly from input video to output signal or heart rate, our modular approach enables each of the three parts of the pipeline to be interpreted individually. The pulse signal estimation module, which we call TURNIP (Time-Series U-Net with Recurrence for Noise-Robust Imaging Photoplethysmography), allows the system to faithfully reconstruct the underlying pulse signal waveform and uses it to measure heart rate and pulse rate variability metrics, even in the presence of motion. When parts of the face are occluded due to extreme head poses, our system explicitly detects such "self-occluded" regions and maintains estimation robustness despite the missing information. Our algorithm provides reliable heart rate estimates without the need for specialized sensors or contact with the skin, outperforming previous iPPG methods on both color (RGB) and near-infrared (NIR) datasets.

Recovering Pulse Waves from Video Using Deep Unrolling and Deep Equilibrium Models

Camera-based monitoring of vital signs, also known as imaging photoplethysmography (iPPG), has seen applications in driver-monitoring, perfusion assessment in surgical settings, affective computing, and more. iPPG involves sensing the underlying cardiac pulse from video of the skin and estimating vital signs such as the heart rate or a full pulse waveform. Some previous iPPG methods impose model-based sparse priors on the pulse signals and use iterative optimization for pulse wave recovery, while others use end-to-end black-box deep learning methods. In contrast, we introduce methods that combine signal processing and deep learning methods in an inverse problem framework. Our methods estimate the underlying pulse signal and heart rate from facial video by learning deep-network-based denoising operators that leverage deep algorithm unfolding and deep equilibrium models. Experiments show that our methods can denoise an acquired signal from the face and infer the correct underlying pulse rate, achieving state-of-the-art heart rate estimation performance on well-known benchmarks, all with less than one-fifth the number of learnable parameters as the closest competing method.

Multi-Band Wi-Fi Neural Dynamic Fusion

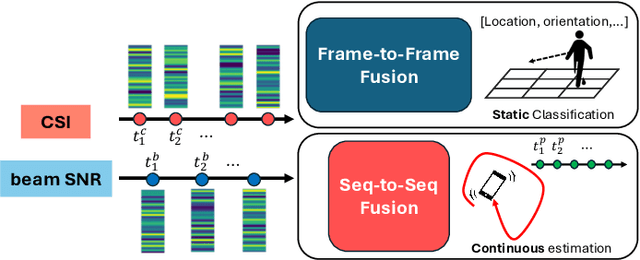
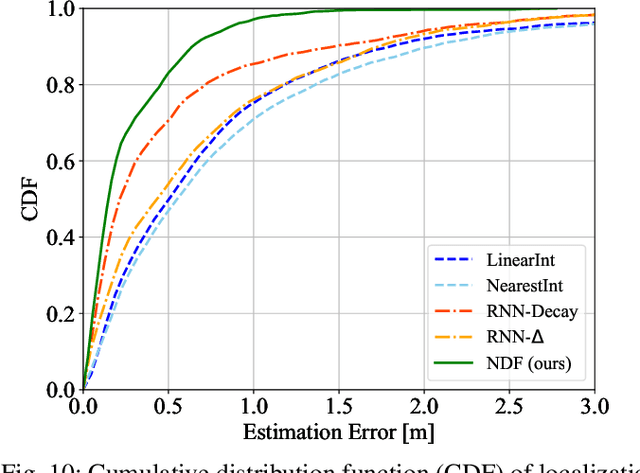
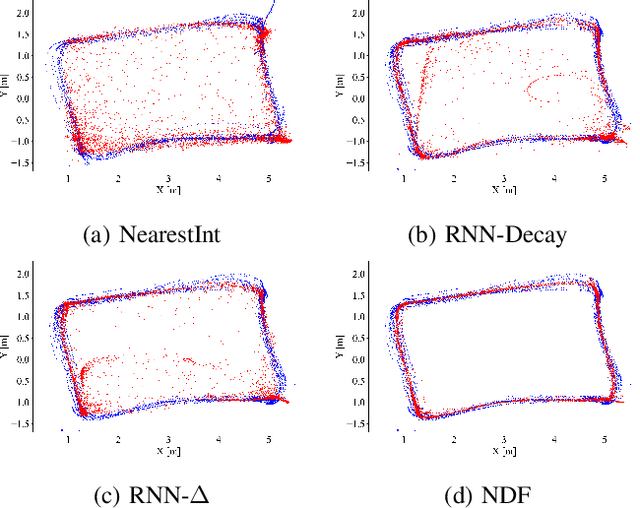
Wi-Fi channel measurements across different bands, e.g., sub-7-GHz and 60-GHz bands, are asynchronous due to the uncoordinated nature of distinct standards protocols, e.g., 802.11ac/ax/be and 802.11ad/ay. Multi-band Wi-Fi fusion has been considered before on a frame-to-frame basis for simple classification tasks, which does not require fine-time-scale alignment. In contrast, this paper considers asynchronous sequence-to-sequence fusion between sub-7-GHz channel state information (CSI) and 60-GHz beam signal-to-noise-ratio~(SNR)s for more challenging tasks such as continuous coordinate estimation. To handle the timing disparity between asynchronous multi-band Wi-Fi channel measurements, this paper proposes a multi-band neural dynamic fusion (NDF) framework. This framework uses separate encoders to embed the multi-band Wi-Fi measurement sequences to separate initial latent conditions. Using a continuous-time ordinary differential equation (ODE) modeling, these initial latent conditions are propagated to respective latent states of the multi-band channel measurements at the same time instances for a latent alignment and a post-ODE fusion, and at their original time instances for measurement reconstruction. We derive a customized loss function based on the variational evidence lower bound (ELBO) that balances between the multi-band measurement reconstruction and continuous coordinate estimation. We evaluate the NDF framework using an in-house multi-band Wi-Fi testbed and demonstrate substantial performance improvements over a comprehensive list of single-band and multi-band baseline methods.

Physics-Informed Koopman Network

Koopman operator theory is receiving increased attention due to its promise to linearize nonlinear dynamics. Neural networks that are developed to represent Koopman operators have shown great success thanks to their ability to approximate arbitrarily complex functions. However, despite their great potential, they typically require large training data-sets either from measurements of a real system or from high-fidelity simulations. In this work, we propose a novel architecture inspired by physics-informed neural networks, which leverage automatic differentiation to impose the underlying physical laws via soft penalty constraints during model training. We demonstrate that it not only reduces the need of large training data-sets, but also maintains high effectiveness in approximating Koopman eigenfunctions.

Fast and High-Quality Blind Multi-Spectral Image Pansharpening

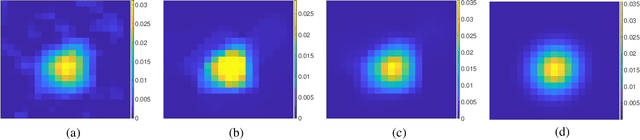
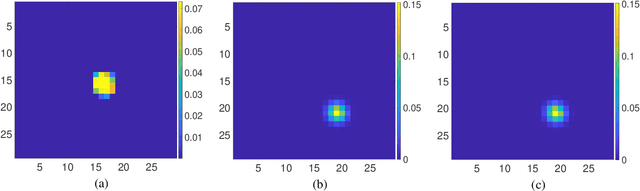
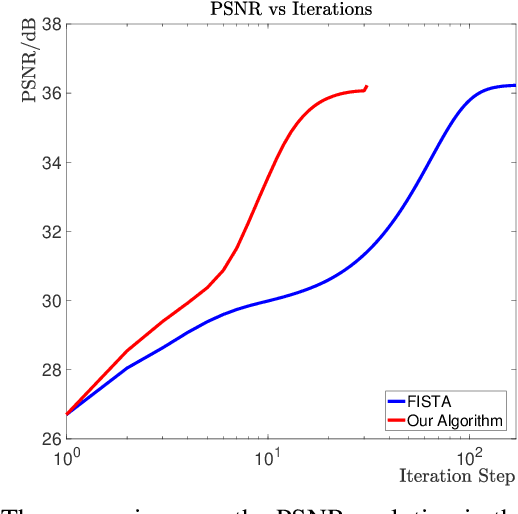
Blind pansharpening addresses the problem of generating a high spatial-resolution multi-spectral (HRMS) image given a low spatial-resolution multi-spectral (LRMS) image with the guidance of its associated spatially misaligned high spatial-resolution panchromatic (PAN) image without parametric side information. In this paper, we propose a fast approach to blind pansharpening and achieve state-of-the-art image reconstruction quality. Typical blind pansharpening algorithms are often computationally intensive since the blur kernel and the target HRMS image are often computed using iterative solvers and in an alternating fashion. To achieve fast blind pansharpening, we decouple the solution of the blur kernel and of the HRMS image. First, we estimate the blur kernel by computing the kernel coefficients with minimum total generalized variation that blur a downsampled version of the PAN image to approximate a linear combination of the LRMS image channels. Then, we estimate each channel of the HRMS image using local Laplacian prior to regularize the relationship between each HRMS channel and the PAN image. Solving the HRMS image is accelerated by both parallelizing across the channels and by fast numerical algorithms for each channel. Due to the fast scheme and the powerful priors we used on the blur kernel coefficients (total generalized variation) and on the cross-channel relationship (local Laplacian prior), numerical experiments demonstrate that our algorithm outperforms state-of-the-art model-based counterparts in terms of both computational time and reconstruction quality of the HRMS images.

Multiview Sensing With Unknown Permutations: An Optimal Transport Approach

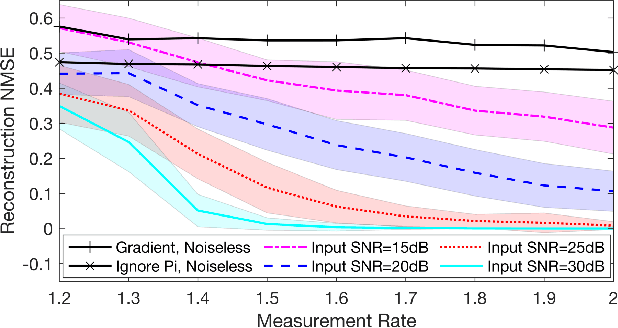
In several applications, including imaging of deformable objects while in motion, simultaneous localization and mapping, and unlabeled sensing, we encounter the problem of recovering a signal that is measured subject to unknown permutations. In this paper we take a fresh look at this problem through the lens of optimal transport (OT). In particular, we recognize that in most practical applications the unknown permutations are not arbitrary but some are more likely to occur than others. We exploit this by introducing a regularization function that promotes the more likely permutations in the solution. We show that, even though the general problem is not convex, an appropriate relaxation of the resulting regularized problem allows us to exploit the well-developed machinery of OT and develop a tractable algorithm.

High-Contrast Limited-Angle Reflection Tomography

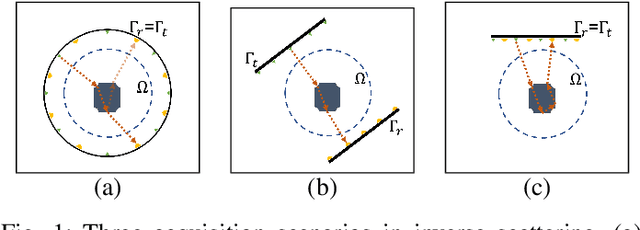
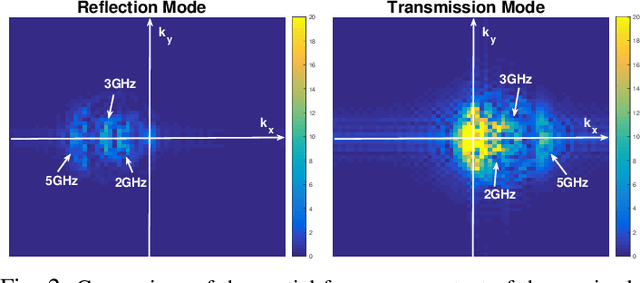
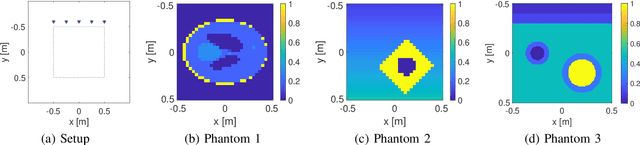
Inverse scattering is the process of estimating the spatial distribution of the scattering potential of an object by measuring the scattered wavefields around it. In this paper, we consider a limited-angle reflection tomography of high contrast objects that commonly occurs in ground-penetrating radar, exploration geophysics, terahertz imaging, ultrasound, and electron microscopy. Unlike conventional transmission tomography, the reflection regime is severely ill-posed since the measured wavefields contain far less spatial frequency information of the target object. We propose a constrained incremental frequency inversion framework that requires no side information from a background model of the object. Our framework solves a sequence of regularized least-squares subproblems that ensure consistency with the measured scattered wavefield while imposing total-variation and non-negativity constraints. We propose a proximal Quasi-Newton method to solve the resulting subproblem and devise an automatic parameter selection routine to determine the constraint of each subproblem. We validate the performance of our approach on synthetic low-resolution phantoms and with a mismatched forward model test on a high-resolution phantom.

On the modes of convergence of Stochastic Optimistic Mirror Descent for saddle point problems

In this article, we study the convergence of Mirror Descent (MD) and Optimistic Mirror Descent (OMD) for saddle point problems satisfying the notion of coherence as proposed in Mertikopoulos et al. We prove convergence of OMD with exact gradients for coherent saddle point problems, and show that monotone convergence only occurs after some sufficiently large number of iterations. This is in contrast to the claim in Mertikopoulos et al. of monotone convergence of OMD with exact gradients for coherent saddle point problems. Besides highlighting this important subtlety, we note that the almost sure convergence guarantees of MD and OMD with stochastic gradients for strictly coherent saddle point problems that are claimed in Mertikopoulos et al. are not fully justified by their proof. As such, we fill out the missing details in the proof and as a result have only been able to prove convergence with high probability. We would like to note that our analysis relies heavily on the core ideas and proof techniques introduced in Zhou et al. and Mertikopoulos et al., and we only aim to re-state and correct the results in light of what we were able to prove rigorously while filling in the much needed missing details in their proofs.