Fast and High-Quality Blind Multi-Spectral Image Pansharpening

Blind pansharpening addresses the problem of generating a high spatial-resolution multi-spectral (HRMS) image given a low spatial-resolution multi-spectral (LRMS) image with the guidance of its associated spatially misaligned high spatial-resolution panchromatic (PAN) image without parametric side information. In this paper, we propose a fast approach to blind pansharpening and achieve state-of-the-art image reconstruction quality. Typical blind pansharpening algorithms are often computationally intensive since the blur kernel and the target HRMS image are often computed using iterative solvers and in an alternating fashion. To achieve fast blind pansharpening, we decouple the solution of the blur kernel and of the HRMS image. First, we estimate the blur kernel by computing the kernel coefficients with minimum total generalized variation that blur a downsampled version of the PAN image to approximate a linear combination of the LRMS image channels. Then, we estimate each channel of the HRMS image using local Laplacian prior to regularize the relationship between each HRMS channel and the PAN image. Solving the HRMS image is accelerated by both parallelizing across the channels and by fast numerical algorithms for each channel. Due to the fast scheme and the powerful priors we used on the blur kernel coefficients (total generalized variation) and on the cross-channel relationship (local Laplacian prior), numerical experiments demonstrate that our algorithm outperforms state-of-the-art model-based counterparts in terms of both computational time and reconstruction quality of the HRMS images.

Multiview Sensing With Unknown Permutations: An Optimal Transport Approach

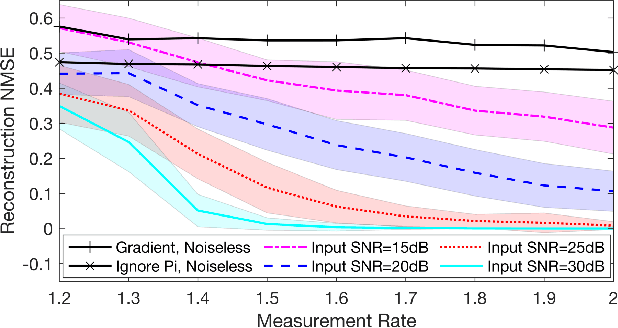
In several applications, including imaging of deformable objects while in motion, simultaneous localization and mapping, and unlabeled sensing, we encounter the problem of recovering a signal that is measured subject to unknown permutations. In this paper we take a fresh look at this problem through the lens of optimal transport (OT). In particular, we recognize that in most practical applications the unknown permutations are not arbitrary but some are more likely to occur than others. We exploit this by introducing a regularization function that promotes the more likely permutations in the solution. We show that, even though the general problem is not convex, an appropriate relaxation of the resulting regularized problem allows us to exploit the well-developed machinery of OT and develop a tractable algorithm.

High-Contrast Limited-Angle Reflection Tomography

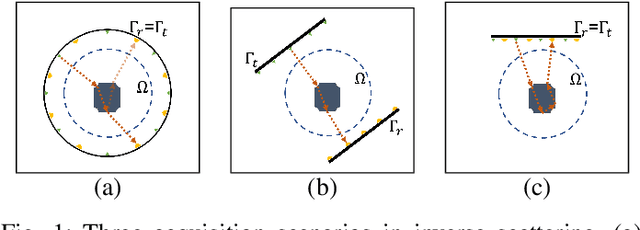
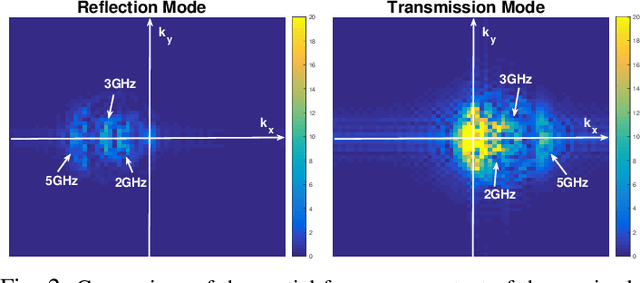
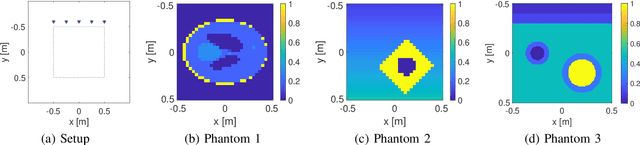
Inverse scattering is the process of estimating the spatial distribution of the scattering potential of an object by measuring the scattered wavefields around it. In this paper, we consider a limited-angle reflection tomography of high contrast objects that commonly occurs in ground-penetrating radar, exploration geophysics, terahertz imaging, ultrasound, and electron microscopy. Unlike conventional transmission tomography, the reflection regime is severely ill-posed since the measured wavefields contain far less spatial frequency information of the target object. We propose a constrained incremental frequency inversion framework that requires no side information from a background model of the object. Our framework solves a sequence of regularized least-squares subproblems that ensure consistency with the measured scattered wavefield while imposing total-variation and non-negativity constraints. We propose a proximal Quasi-Newton method to solve the resulting subproblem and devise an automatic parameter selection routine to determine the constraint of each subproblem. We validate the performance of our approach on synthetic low-resolution phantoms and with a mismatched forward model test on a high-resolution phantom.

Sparse Blind Deconvolution for Distributed Radar Autofocus Imaging

A common problem that arises in radar imaging systems, especially those mounted on mobile platforms, is antenna position ambiguity. Approaches to resolve this ambiguity and correct position errors are generally known as radar autofocus. Common techniques that attempt to resolve the antenna ambiguity generally assume an unknown gain and phase error afflicting the radar measurements. However, ensuring identifiability and tractability of the unknown error imposes strict restrictions on the allowable antenna perturbations. Furthermore, these techniques are often not applicable in near-field imaging, where mapping the position ambiguity to phase errors breaks down. In this paper, we propose an alternate formulation where the position error of each antenna is mapped to a spatial shift operator in the image-domain. Thus, the radar autofocus problem becomes a multichannel blind deconvolution problem, in which the radar measurements correspond to observations of a static radar image that is convolved with the spatial shift kernel associated with each antenna. To solve the reformulated problem, we also develop a block coordinate descent framework that leverages the sparsity and piece-wise smoothness of the radar scene, as well as the one-sparse property of the two dimensional shift kernels. We evaluate the performance of our approach using both simulated and experimental radar measurements, and demonstrate its superior performance compared to state-of-the-art methods.

Accelerated Image Reconstruction for Nonlinear Diffractive Imaging

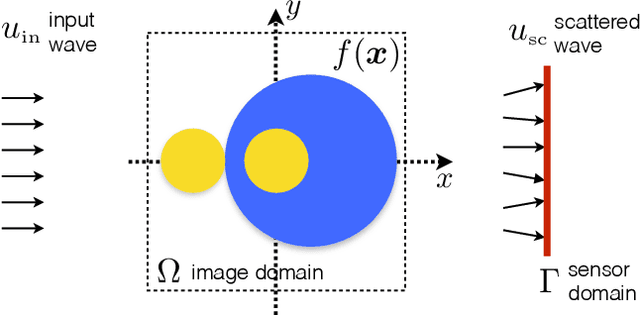
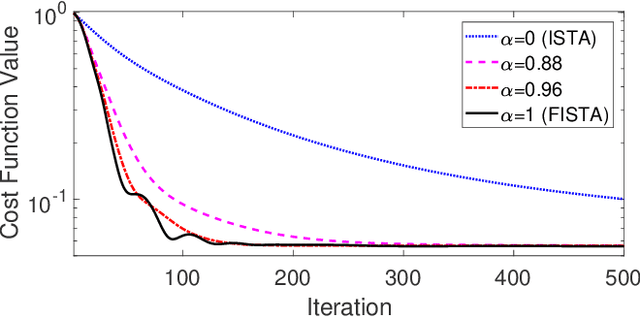
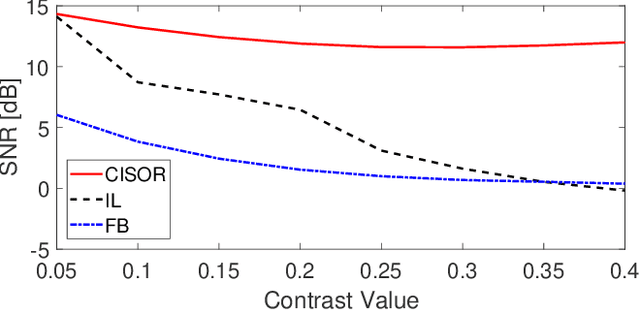
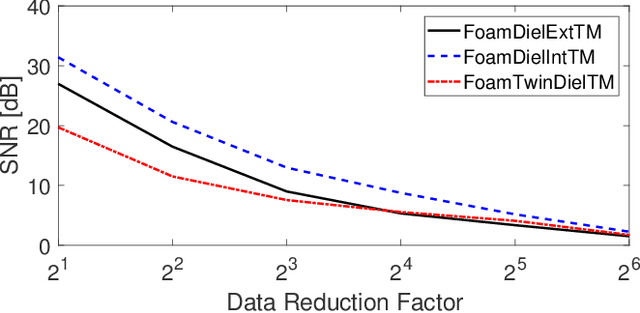
The problem of reconstructing an object from the measurements of the light it scatters is common in numerous imaging applications. While the most popular formulations of the problem are based on linearizing the object-light relationship, there is an increased interest in considering nonlinear formulations that can account for multiple light scattering. In this paper, we propose an image reconstruction method, called CISOR, for nonlinear diffractive imaging, based on a nonconvex optimization formulation with total variation (TV) regularization. The nonconvex solver used in CISOR is our new variant of fast iterative shrinkage/thresholding algorithm (FISTA). We provide fast and memory-efficient implementation of the new FISTA variant and prove that it reliably converges for our nonconvex optimization problem. In addition, we systematically compare our method with other state-of-the-art methods on simulated as well as experimentally measured data in both 2D and 3D settings.

Online Convolutional Dictionary Learning for Multimodal Imaging

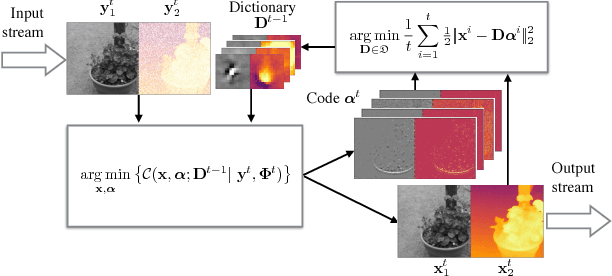
Computational imaging methods that can exploit multiple modalities have the potential to enhance the capabilities of traditional sensing systems. In this paper, we propose a new method that reconstructs multimodal images from their linear measurements by exploiting redundancies across different modalities. Our method combines a convolutional group-sparse representation of images with total variation (TV) regularization for high-quality multimodal imaging. We develop an online algorithm that enables the unsupervised learning of convolutional dictionaries on large-scale datasets that are typical in such applications. We illustrate the benefit of our approach in the context of joint intensity-depth imaging.

SEAGLE: Sparsity-Driven Image Reconstruction under Multiple Scattering

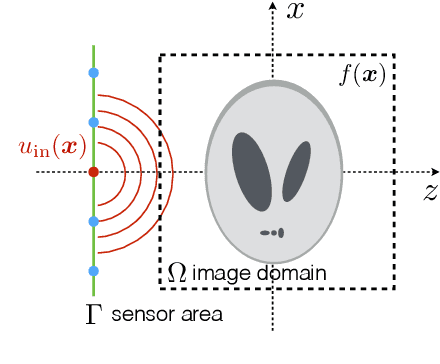
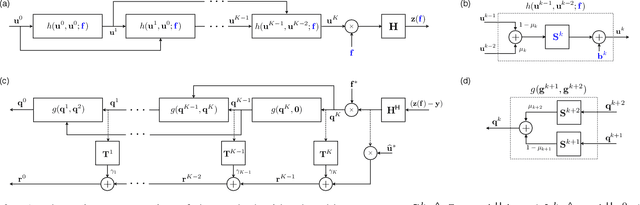
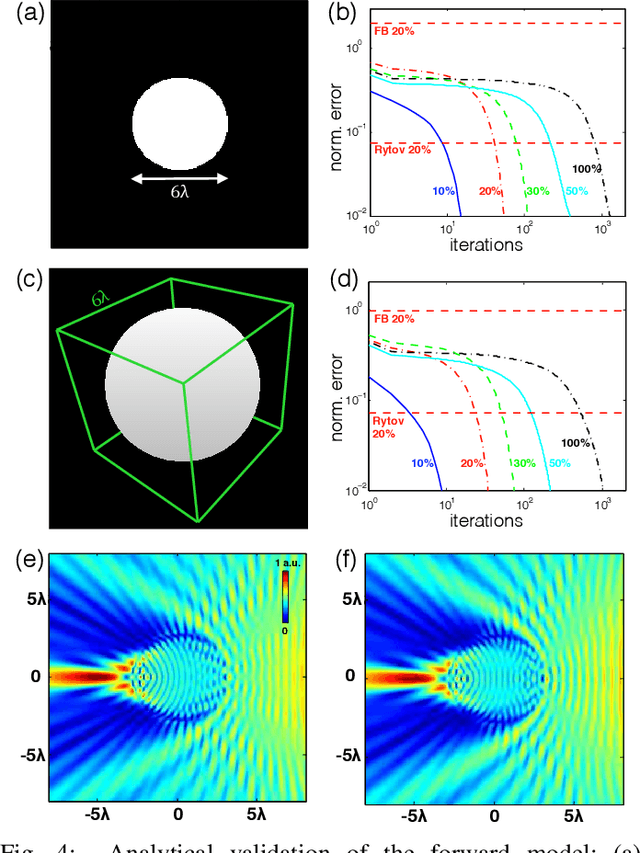
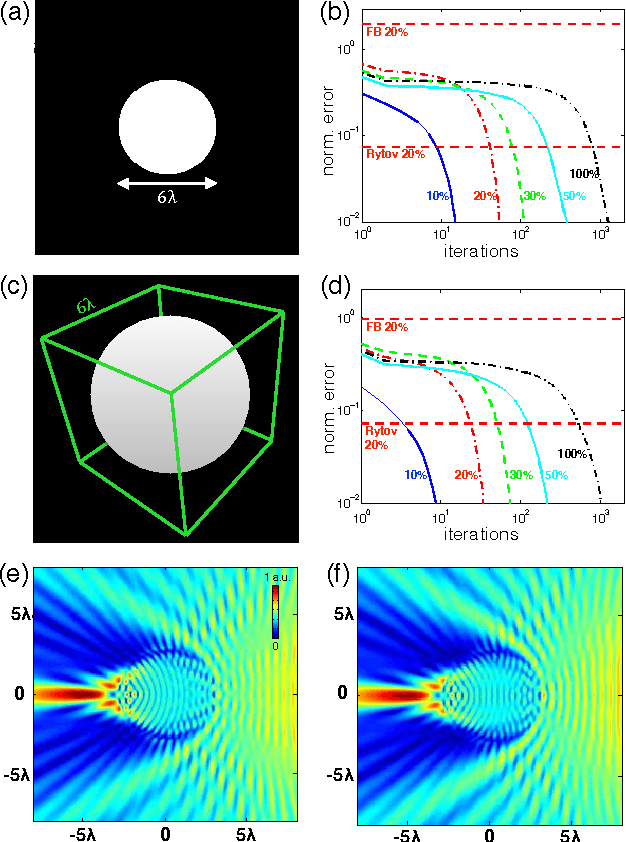
Multiple scattering of an electromagnetic wave as it passes through an object is a fundamental problem that limits the performance of current imaging systems. In this paper, we describe a new technique-called Series Expansion with Accelerated Gradient Descent on Lippmann-Schwinger Equation (SEAGLE)-for robust imaging under multiple scattering based on a combination of a new nonlinear forward model and a total variation (TV) regularizer. The proposed forward model can account for multiple scattering, which makes it advantageous in applications where linear models are inaccurate. Specifically, it corresponds to a series expansion of the scattered wave with an accelerated-gradient method. This expansion guarantees the convergence even for strongly scattering objects. One of our key insights is that it is possible to obtain an explicit formula for computing the gradient of our nonlinear forward model with respect to the unknown object, thus enabling fast image reconstruction with the state-of-the-art fast iterative shrinkage/thresholding algorithm (FISTA). The proposed method is validated on both simulated and experimentally measured data.

Compressive Imaging with Iterative Forward Models

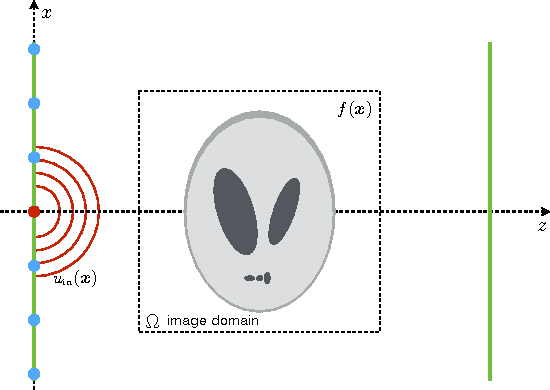
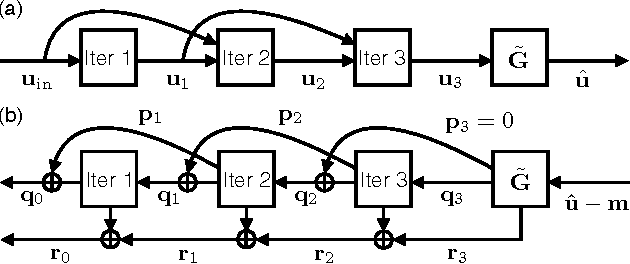
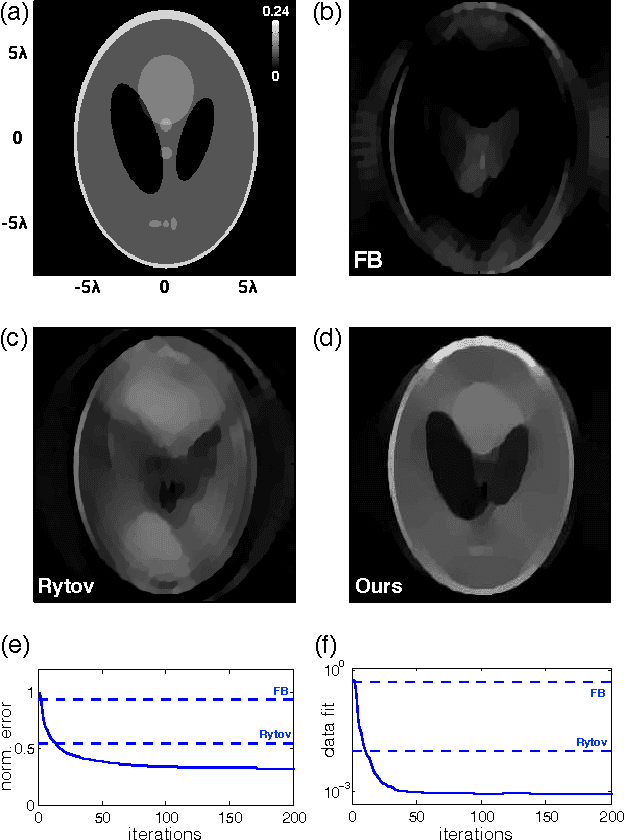
We propose a new compressive imaging method for reconstructing 2D or 3D objects from their scattered wave-field measurements. Our method relies on a novel, nonlinear measurement model that can account for the multiple scattering phenomenon, which makes the method preferable in applications where linear measurement models are inaccurate. We construct the measurement model by expanding the scattered wave-field with an accelerated-gradient method, which is guaranteed to converge and is suitable for large-scale problems. We provide explicit formulas for computing the gradient of our measurement model with respect to the unknown image, which enables image formation with a sparsity- driven numerical optimization algorithm. We validate the method both analytically and with numerical simulations.

A Recursive Born Approach to Nonlinear Inverse Scattering

The Iterative Born Approximation (IBA) is a well-known method for describing waves scattered by semi-transparent objects. In this paper, we present a novel nonlinear inverse scattering method that combines IBA with an edge-preserving total variation (TV) regularizer. The proposed method is obtained by relating iterations of IBA to layers of a feedforward neural network and developing a corresponding error backpropagation algorithm for efficiently estimating the permittivity of the object. Simulations illustrate that, by accounting for multiple scattering, the method successfully recovers the permittivity distribution where the traditional linear inverse scattering fails.

Depth Superresolution using Motion Adaptive Regularization

Spatial resolution of depth sensors is often significantly lower compared to that of conventional optical cameras. Recent work has explored the idea of improving the resolution of depth using higher resolution intensity as a side information. In this paper, we demonstrate that further incorporating temporal information in videos can significantly improve the results. In particular, we propose a novel approach that improves depth resolution, exploiting the space-time redundancy in the depth and intensity using motion-adaptive low-rank regularization. Experiments confirm that the proposed approach substantially improves the quality of the estimated high-resolution depth. Our approach can be a first component in systems using vision techniques that rely on high resolution depth information.