Single-shot Tomography of Discrete Dynamic Objects

This paper presents a novel method for the reconstruction of high-resolution temporal images in dynamic tomographic imaging, particularly for discrete objects with smooth boundaries that vary over time. Addressing the challenge of limited measurements per time point, we propose a technique that synergistically incorporates spatial and temporal information of the dynamic objects. This is achieved through the application of the level-set method for image segmentation and the representation of motion via a sinusoidal basis. The result is a computationally efficient and easily optimizable variational framework that enables the reconstruction of high-quality 2D or 3D image sequences with a single projection per frame. Compared to current methods, our proposed approach demonstrates superior performance on both synthetic and pseudo-dynamic real X-ray tomography datasets. The implications of this research extend to improved visualization and analysis of dynamic processes in tomographic imaging, finding potential applications in diverse scientific and industrial domains.

ADJUST: A Dictionary-Based Joint Reconstruction and Unmixing Method for Spectral Tomography

Advances in multi-spectral detectors are causing a paradigm shift in X-ray Computed Tomography (CT). Spectral information acquired from these detectors can be used to extract volumetric material composition maps of the object of interest. If the materials and their spectral responses are known a priori, the image reconstruction step is rather straightforward. If they are not known, however, the maps as well as the responses need to be estimated jointly. A conventional workflow in spectral CT involves performing volume reconstruction followed by material decomposition, or vice versa. However, these methods inherently suffer from the ill-posedness of the joint reconstruction problem. To resolve this issue, we propose `A Dictionary-based Joint reconstruction and Unmixing method for Spectral Tomography' (ADJUST). Our formulation relies on forming a dictionary of spectral signatures of materials common in CT and prior knowledge of the number of materials present in an object. In particular, we decompose the spectral volume linearly in terms of spatial material maps, a spectral dictionary, and the indicator of materials for the dictionary elements. We propose a memory-efficient accelerated alternating proximal gradient method to find an approximate solution to the resulting bi-convex problem. From numerical demonstrations on several synthetic phantoms, we observe that ADJUST performs exceedingly well when compared to other state-of-the-art methods. Additionally, we address the robustness of ADJUST against limited measurement patterns.

CoShaRP: A Convex Program for Single-shot Tomographic Shape Sensing

We introduce single-shot X-ray tomography that aims to estimate the target image from a single cone-beam projection measurement. This linear inverse problem is extremely under-determined since the measurements are far fewer than the number of unknowns. Moreover, it is more challenging than conventional tomography where a sufficiently large number of projection angles forms the measurements, allowing for a simple inversion process. However, single-shot tomography becomes less severe if the target image is only composed of known shapes. Hence, the shape prior transforms a linear ill-posed image estimation problem to a non-linear problem of estimating the roto-translations of the shapes. In this paper, we circumvent the non-linearity by using a dictionary of possible roto-translations of the shapes. We propose a convex program CoShaRP to recover the dictionary-coefficients successfully. CoShaRP relies on simplex-type constraint and can be solved quickly using a primal-dual algorithm. The numerical experiments show that CoShaRP recovers shapes stably from moderately noisy measurements.

High-Contrast Limited-Angle Reflection Tomography

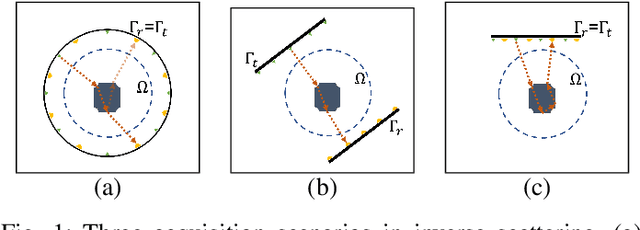
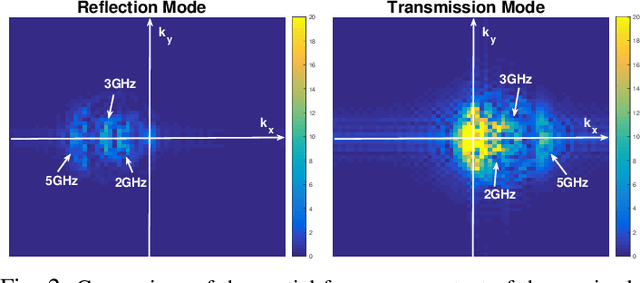
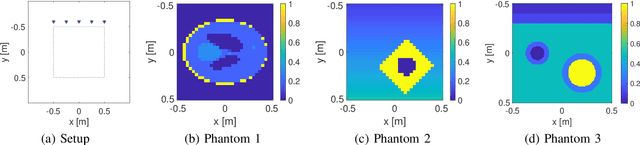
Inverse scattering is the process of estimating the spatial distribution of the scattering potential of an object by measuring the scattered wavefields around it. In this paper, we consider a limited-angle reflection tomography of high contrast objects that commonly occurs in ground-penetrating radar, exploration geophysics, terahertz imaging, ultrasound, and electron microscopy. Unlike conventional transmission tomography, the reflection regime is severely ill-posed since the measured wavefields contain far less spatial frequency information of the target object. We propose a constrained incremental frequency inversion framework that requires no side information from a background model of the object. Our framework solves a sequence of regularized least-squares subproblems that ensure consistency with the measured scattered wavefield while imposing total-variation and non-negativity constraints. We propose a proximal Quasi-Newton method to solve the resulting subproblem and devise an automatic parameter selection routine to determine the constraint of each subproblem. We validate the performance of our approach on synthetic low-resolution phantoms and with a mismatched forward model test on a high-resolution phantom.