SEAGLE: Sparsity-Driven Image Reconstruction under Multiple Scattering

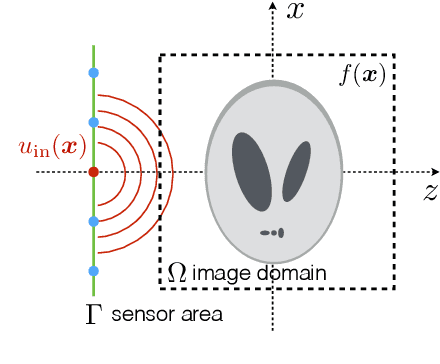
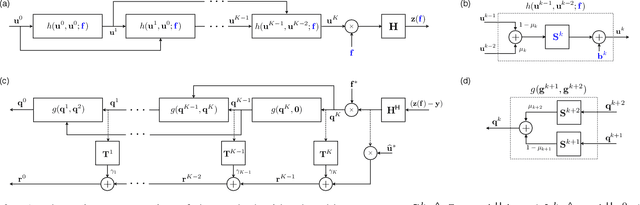
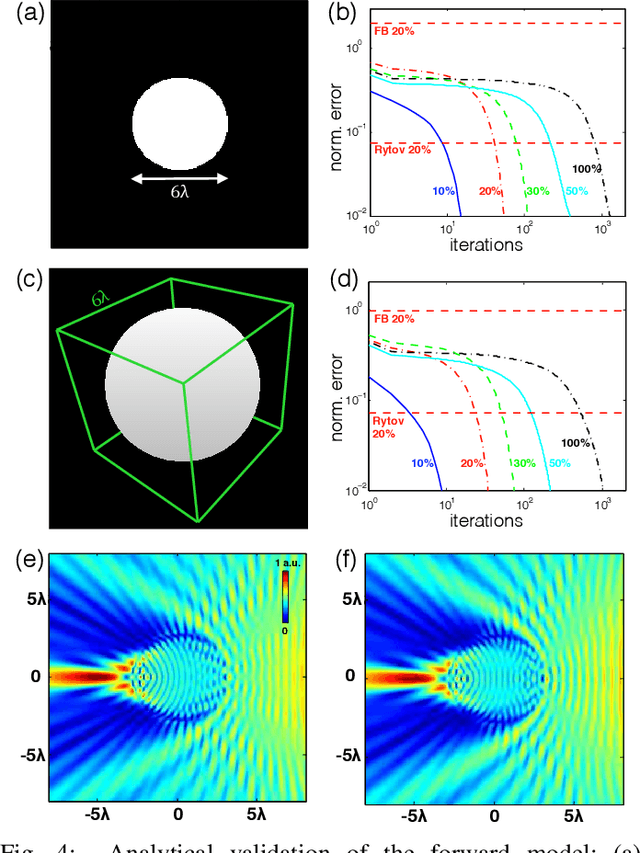
Multiple scattering of an electromagnetic wave as it passes through an object is a fundamental problem that limits the performance of current imaging systems. In this paper, we describe a new technique-called Series Expansion with Accelerated Gradient Descent on Lippmann-Schwinger Equation (SEAGLE)-for robust imaging under multiple scattering based on a combination of a new nonlinear forward model and a total variation (TV) regularizer. The proposed forward model can account for multiple scattering, which makes it advantageous in applications where linear models are inaccurate. Specifically, it corresponds to a series expansion of the scattered wave with an accelerated-gradient method. This expansion guarantees the convergence even for strongly scattering objects. One of our key insights is that it is possible to obtain an explicit formula for computing the gradient of our nonlinear forward model with respect to the unknown object, thus enabling fast image reconstruction with the state-of-the-art fast iterative shrinkage/thresholding algorithm (FISTA). The proposed method is validated on both simulated and experimentally measured data.

Compressive Imaging with Iterative Forward Models

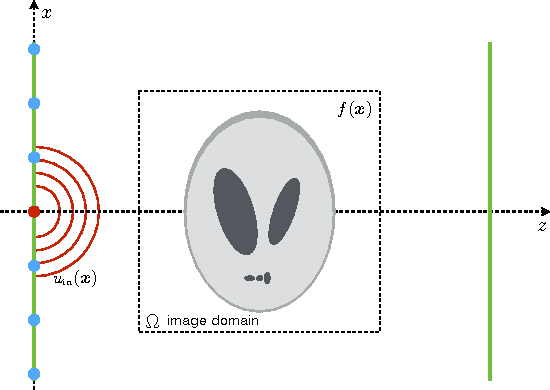
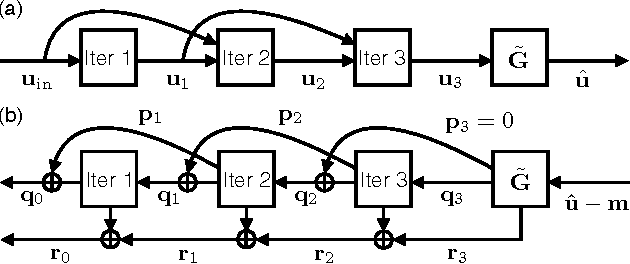
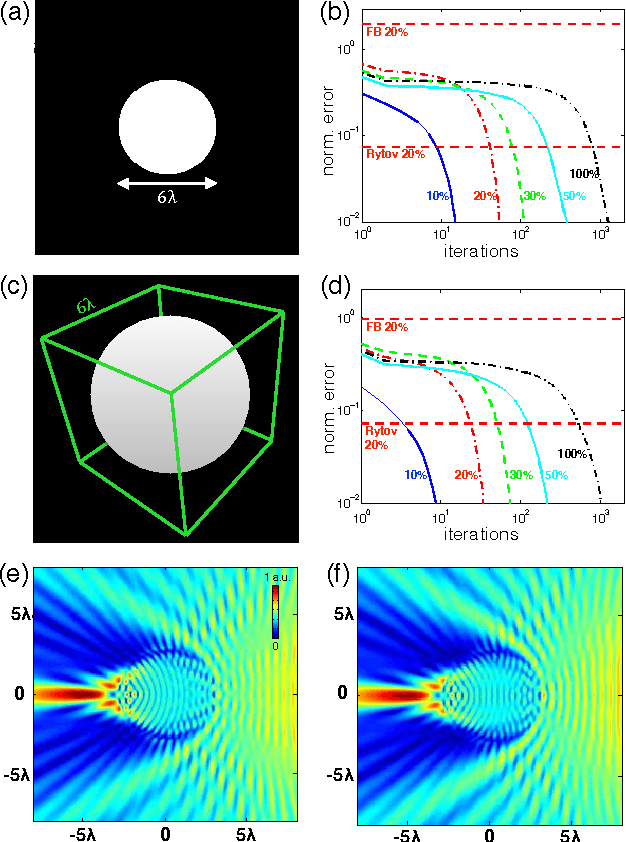
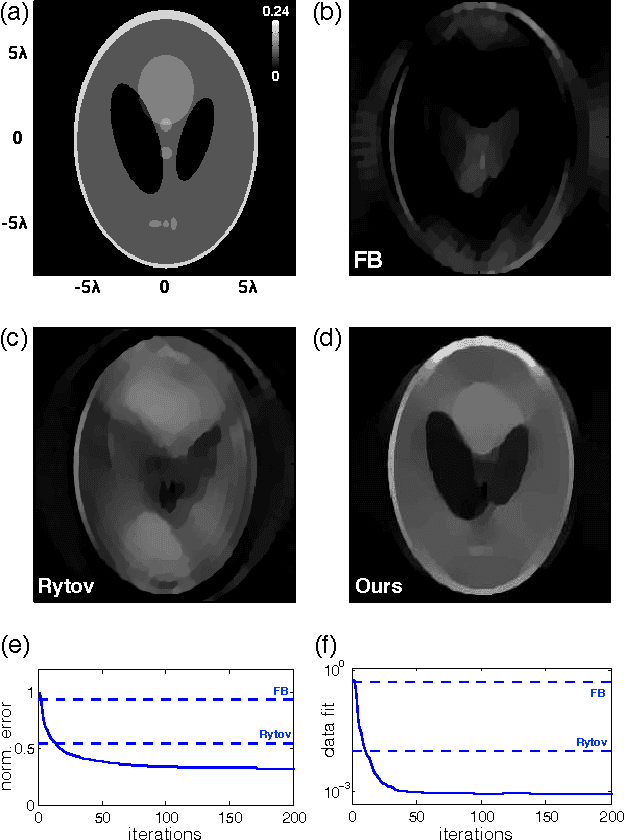
We propose a new compressive imaging method for reconstructing 2D or 3D objects from their scattered wave-field measurements. Our method relies on a novel, nonlinear measurement model that can account for the multiple scattering phenomenon, which makes the method preferable in applications where linear measurement models are inaccurate. We construct the measurement model by expanding the scattered wave-field with an accelerated-gradient method, which is guaranteed to converge and is suitable for large-scale problems. We provide explicit formulas for computing the gradient of our measurement model with respect to the unknown image, which enables image formation with a sparsity- driven numerical optimization algorithm. We validate the method both analytically and with numerical simulations.