Data-driven control of COVID-19 in buildings: a reinforcement-learning approach

In addition to its public health crisis, COVID-19 pandemic has led to the shutdown and closure of workplaces with an estimated total cost of more than $16 trillion. Given the long hours an average person spends in buildings and indoor environments, this research article proposes data-driven control strategies to design optimal indoor airflow to minimize the exposure of occupants to viral pathogens in built environments. A general control framework is put forward for designing an optimal velocity field and proximal policy optimization, a reinforcement learning algorithm is employed to solve the control problem in a data-driven fashion. The same framework is used for optimal placement of disinfectants to neutralize the viral pathogens as an alternative to the airflow design when the latter is practically infeasible or hard to implement. We show, via simulation experiments, that the control agent learns the optimal policy in both scenarios within a reasonable time. The proposed data-driven control framework in this study will have significant societal and economic benefits by setting the foundation for an improved methodology in designing case-specific infection control guidelines that can be realized by affordable ventilation devices and disinfectants.

Physics-Informed Koopman Network

Koopman operator theory is receiving increased attention due to its promise to linearize nonlinear dynamics. Neural networks that are developed to represent Koopman operators have shown great success thanks to their ability to approximate arbitrarily complex functions. However, despite their great potential, they typically require large training data-sets either from measurements of a real system or from high-fidelity simulations. In this work, we propose a novel architecture inspired by physics-informed neural networks, which leverage automatic differentiation to impose the underlying physical laws via soft penalty constraints during model training. We demonstrate that it not only reduces the need of large training data-sets, but also maintains high effectiveness in approximating Koopman eigenfunctions.

Reinforcement Learning with Function-Valued Action Spaces for Partial Differential Equation Control

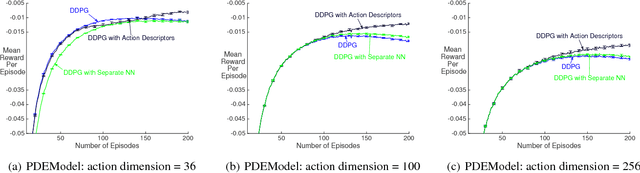
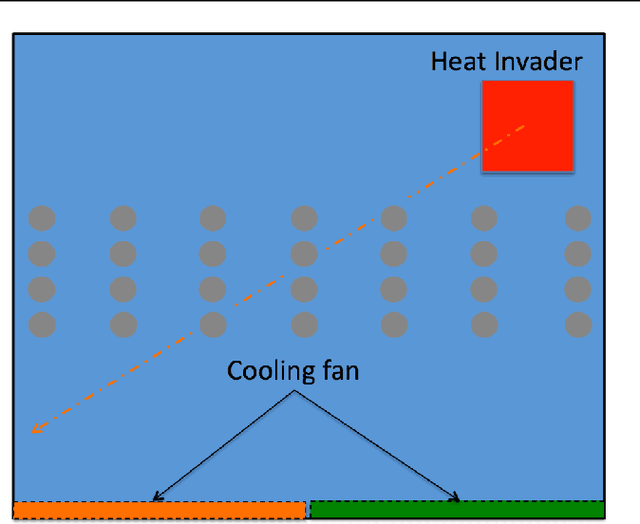
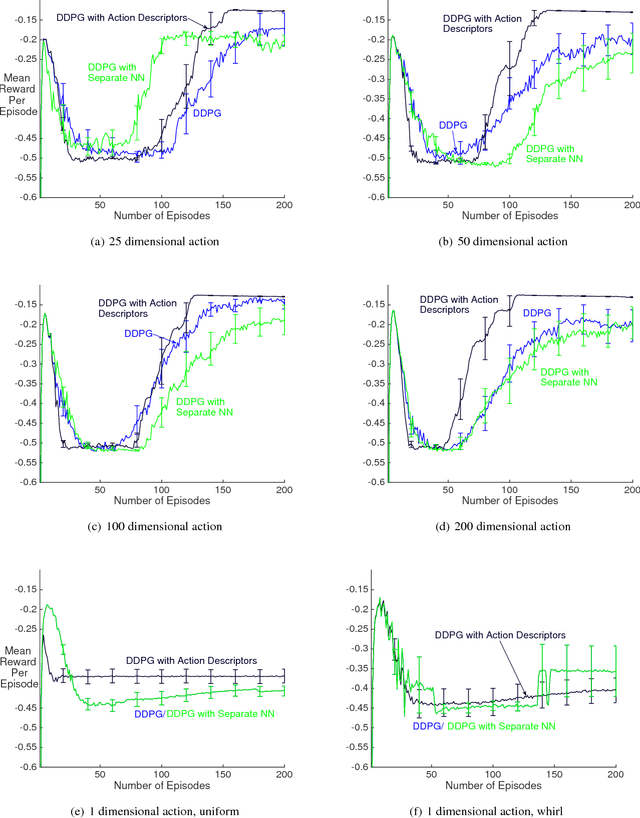
Recent work has shown that reinforcement learning (RL) is a promising approach to control dynamical systems described by partial differential equations (PDE). This paper shows how to use RL to tackle more general PDE control problems that have continuous high-dimensional action spaces with spatial relationship among action dimensions. In particular, we propose the concept of action descriptors, which encode regularities among spatially-extended action dimensions and enable the agent to control high-dimensional action PDEs. We provide theoretical evidence suggesting that this approach can be more sample efficient compared to a conventional approach that treats each action dimension separately and does not explicitly exploit the spatial regularity of the action space. The action descriptor approach is then used within the deep deterministic policy gradient algorithm. Experiments on two PDE control problems, with up to 256-dimensional continuous actions, show the advantage of the proposed approach over the conventional one.