Physics-Informed Koopman Network

Koopman operator theory is receiving increased attention due to its promise to linearize nonlinear dynamics. Neural networks that are developed to represent Koopman operators have shown great success thanks to their ability to approximate arbitrarily complex functions. However, despite their great potential, they typically require large training data-sets either from measurements of a real system or from high-fidelity simulations. In this work, we propose a novel architecture inspired by physics-informed neural networks, which leverage automatic differentiation to impose the underlying physical laws via soft penalty constraints during model training. We demonstrate that it not only reduces the need of large training data-sets, but also maintains high effectiveness in approximating Koopman eigenfunctions.

Hierarchical Deep Learning of Multiscale Differential Equation Time-Steppers

Nonlinear differential equations rarely admit closed-form solutions, thus requiring numerical time-stepping algorithms to approximate solutions. Further, many systems characterized by multiscale physics exhibit dynamics over a vast range of timescales, making numerical integration computationally expensive due to numerical stiffness. In this work, we develop a hierarchy of deep neural network time-steppers to approximate the flow map of the dynamical system over a disparate range of time-scales. The resulting model is purely data-driven and leverages features of the multiscale dynamics, enabling numerical integration and forecasting that is both accurate and highly efficient. Moreover, similar ideas can be used to couple neural network-based models with classical numerical time-steppers. Our multiscale hierarchical time-stepping scheme provides important advantages over current time-stepping algorithms, including (i) circumventing numerical stiffness due to disparate time-scales, (ii) improved accuracy in comparison with leading neural-network architectures, (iii) efficiency in long-time simulation/forecasting due to explicit training of slow time-scale dynamics, and (iv) a flexible framework that is parallelizable and may be integrated with standard numerical time-stepping algorithms. The method is demonstrated on a wide range of nonlinear dynamical systems, including the Van der Pol oscillator, the Lorenz system, the Kuramoto-Sivashinsky equation, and fluid flow pass a cylinder; audio and video signals are also explored. On the sequence generation examples, we benchmark our algorithm against state-of-the-art methods, such as LSTM, reservoir computing, and clockwork RNN. Despite the structural simplicity of our method, it outperforms competing methods on numerical integration.

Multiresolution Convolutional Autoencoders

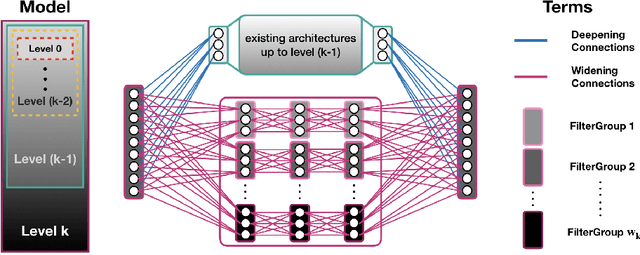
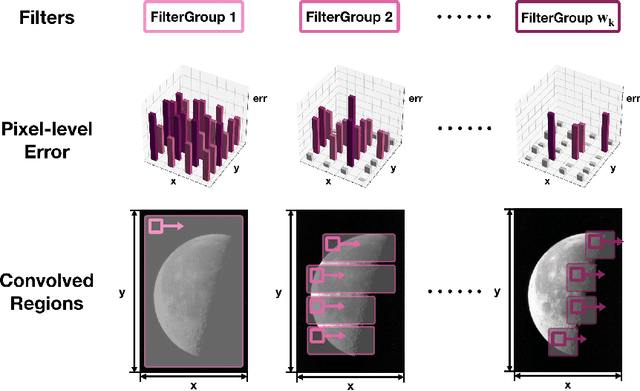
We propose a multi-resolution convolutional autoencoder (MrCAE) architecture that integrates and leverages three highly successful mathematical architectures: (i) multigrid methods, (ii) convolutional autoencoders and (iii) transfer learning. The method provides an adaptive, hierarchical architecture that capitalizes on a progressive training approach for multiscale spatio-temporal data. This framework allows for inputs across multiple scales: starting from a compact (small number of weights) network architecture and low-resolution data, our network progressively deepens and widens itself in a principled manner to encode new information in the higher resolution data based on its current performance of reconstruction. Basic transfer learning techniques are applied to ensure information learned from previous training steps can be rapidly transferred to the larger network. As a result, the network can dynamically capture different scaled features at different depths of the network. The performance gains of this adaptive multiscale architecture are illustrated through a sequence of numerical experiments on synthetic examples and real-world spatial-temporal data.