Reinforcement Learning with Function-Valued Action Spaces for Partial Differential Equation Control

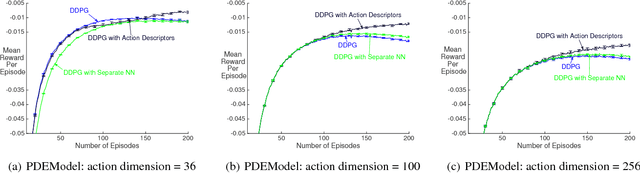
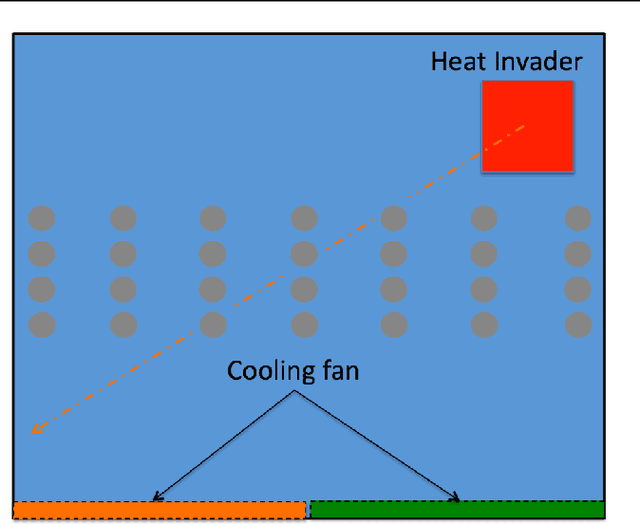
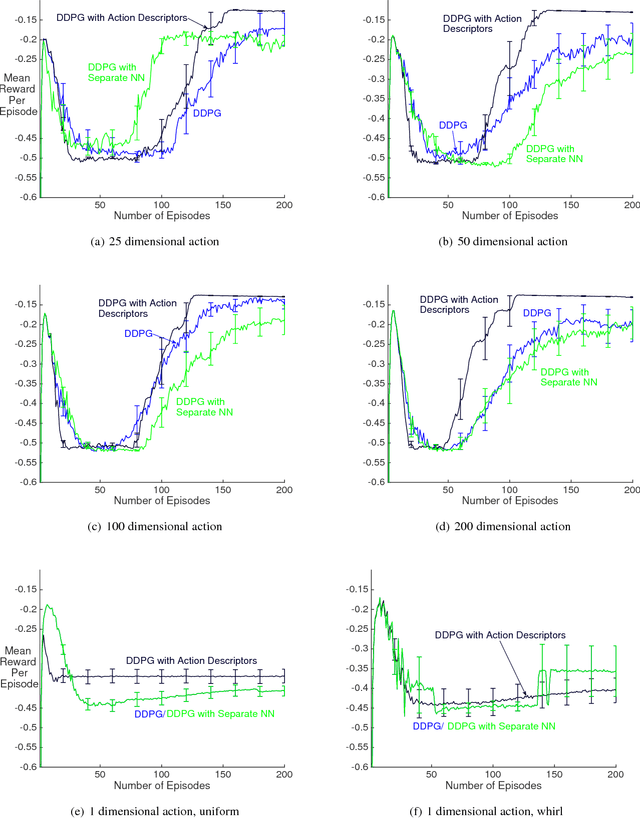
Recent work has shown that reinforcement learning (RL) is a promising approach to control dynamical systems described by partial differential equations (PDE). This paper shows how to use RL to tackle more general PDE control problems that have continuous high-dimensional action spaces with spatial relationship among action dimensions. In particular, we propose the concept of action descriptors, which encode regularities among spatially-extended action dimensions and enable the agent to control high-dimensional action PDEs. We provide theoretical evidence suggesting that this approach can be more sample efficient compared to a conventional approach that treats each action dimension separately and does not explicitly exploit the spatial regularity of the action space. The action descriptor approach is then used within the deep deterministic policy gradient algorithm. Experiments on two PDE control problems, with up to 256-dimensional continuous actions, show the advantage of the proposed approach over the conventional one.

Model-free control framework for multi-limb soft robots

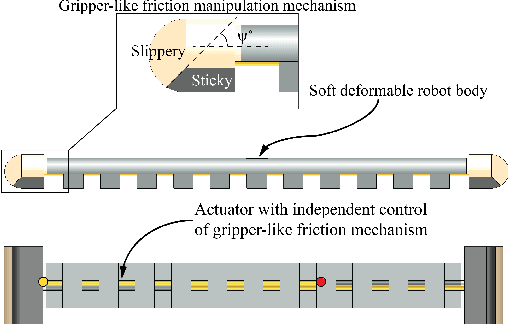
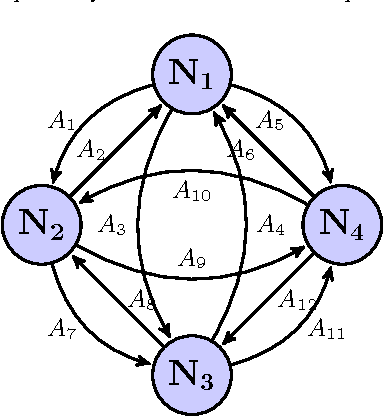
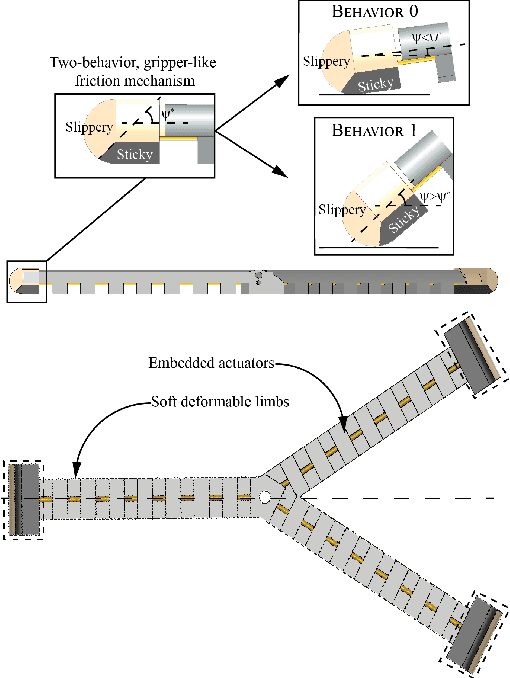
The deformable and continuum nature of soft robots promises versatility and adaptability. However, control of modular, multi-limbed soft robots for terrestrial locomotion is challenging due to the complex robot structure, actuator mechanics and robot-environment interaction. Traditionally, soft robot control is performed by modeling kinematics using exact geometric equations and finite element analysis. The research presents an alternative, model-free, data-driven, reinforcement learning inspired approach, for controlling multi-limbed soft material robots. This control approach can be summarized as a four-step process of discretization, visualization, learning and optimization. The first step involves identification and subsequent discretization of key factors that dominate robot-environment, in turn, the robot control. Graph theory is used to visualize relationships and transitions between the discretized states. The graph representation facilitates mathematical definition of periodic control patterns (simple cycles) and locomotion gaits. Rewards corresponding to individual arcs of the graph are weighted displacement and orientation change for robot state-to-state transitions. These rewards are specific to surface of locomotion and are learned. Finally, the control patterns result from optimization of reward dependent locomotion task (e.g. translation) cost function. The optimization problem is an Integer Linear Programming problem which can be quickly solved using standard solvers. The framework is generic and independent of type of actuator, soft material properties or the type of friction mechanism, as the control exists in the robot's task space. Furthermore, the data-driven nature of the framework imparts adaptability to the framework toward different locomotion surfaces by re-learning rewards.