Enhancing Privacy in Decentralized Min-Max Optimization: A Differentially Private Approach

Decentralized min-max optimization allows multi-agent systems to collaboratively solve global min-max optimization problems by facilitating the exchange of model updates among neighboring agents, eliminating the need for a central server. However, sharing model updates in such systems carry a risk of exposing sensitive data to inference attacks, raising significant privacy concerns. To mitigate these privacy risks, differential privacy (DP) has become a widely adopted technique for safeguarding individual data. Despite its advantages, implementing DP in decentralized min-max optimization poses challenges, as the added noise can hinder convergence, particularly in non-convex scenarios with complex agent interactions in min-max optimization problems. In this work, we propose an algorithm called DPMixSGD (Differential Private Minmax Hybrid Stochastic Gradient Descent), a novel privacy-preserving algorithm specifically designed for non-convex decentralized min-max optimization. Our method builds on the state-of-the-art STORM-based algorithm, one of the fastest decentralized min-max solutions. We rigorously prove that the noise added to local gradients does not significantly compromise convergence performance, and we provide theoretical bounds to ensure privacy guarantees. To validate our theoretical findings, we conduct extensive experiments across various tasks and models, demonstrating the effectiveness of our approach.

Benchmarking Poisoning Attacks against Retrieval-Augmented Generation

Retrieval-Augmented Generation (RAG) has proven effective in mitigating hallucinations in large language models by incorporating external knowledge during inference. However, this integration introduces new security vulnerabilities, particularly to poisoning attacks. Although prior work has explored various poisoning strategies, a thorough assessment of their practical threat to RAG systems remains missing. To address this gap, we propose the first comprehensive benchmark framework for evaluating poisoning attacks on RAG. Our benchmark covers 5 standard question answering (QA) datasets and 10 expanded variants, along with 13 poisoning attack methods and 7 defense mechanisms, representing a broad spectrum of existing techniques. Using this benchmark, we conduct a comprehensive evaluation of all included attacks and defenses across the full dataset spectrum. Our findings show that while existing attacks perform well on standard QA datasets, their effectiveness drops significantly on the expanded versions. Moreover, our results demonstrate that various advanced RAG architectures, such as sequential, branching, conditional, and loop RAG, as well as multi-turn conversational RAG, multimodal RAG systems, and RAG-based LLM agent systems, remain susceptible to poisoning attacks. Notably, current defense techniques fail to provide robust protection, underscoring the pressing need for more resilient and generalizable defense strategies.

Toward Malicious Clients Detection in Federated Learning

Federated learning (FL) enables multiple clients to collaboratively train a global machine learning model without sharing their raw data. However, the decentralized nature of FL introduces vulnerabilities, particularly to poisoning attacks, where malicious clients manipulate their local models to disrupt the training process. While Byzantine-robust aggregation rules have been developed to mitigate such attacks, they remain inadequate against more advanced threats. In response, recent advancements have focused on FL detection techniques to identify potentially malicious participants. Unfortunately, these methods often misclassify numerous benign clients as threats or rely on unrealistic assumptions about the server's capabilities. In this paper, we propose a novel algorithm, SafeFL, specifically designed to accurately identify malicious clients in FL. The SafeFL approach involves the server collecting a series of global models to generate a synthetic dataset, which is then used to distinguish between malicious and benign models based on their behavior. Extensive testing demonstrates that SafeFL outperforms existing methods, offering superior efficiency and accuracy in detecting malicious clients.

Traceback of Poisoning Attacks to Retrieval-Augmented Generation

Large language models (LLMs) integrated with retrieval-augmented generation (RAG) systems improve accuracy by leveraging external knowledge sources. However, recent research has revealed RAG's susceptibility to poisoning attacks, where the attacker injects poisoned texts into the knowledge database, leading to attacker-desired responses. Existing defenses, which predominantly focus on inference-time mitigation, have proven insufficient against sophisticated attacks. In this paper, we introduce RAGForensics, the first traceback system for RAG, designed to identify poisoned texts within the knowledge database that are responsible for the attacks. RAGForensics operates iteratively, first retrieving a subset of texts from the database and then utilizing a specially crafted prompt to guide an LLM in detecting potential poisoning texts. Empirical evaluations across multiple datasets demonstrate the effectiveness of RAGForensics against state-of-the-art poisoning attacks. This work pioneers the traceback of poisoned texts in RAG systems, providing a practical and promising defense mechanism to enhance their security.

Practical Poisoning Attacks against Retrieval-Augmented Generation

Large language models (LLMs) have demonstrated impressive natural language processing abilities but face challenges such as hallucination and outdated knowledge. Retrieval-Augmented Generation (RAG) has emerged as a state-of-the-art approach to mitigate these issues. While RAG enhances LLM outputs, it remains vulnerable to poisoning attacks. Recent studies show that injecting poisoned text into the knowledge database can compromise RAG systems, but most existing attacks assume that the attacker can insert a sufficient number of poisoned texts per query to outnumber correct-answer texts in retrieval, an assumption that is often unrealistic. To address this limitation, we propose CorruptRAG, a practical poisoning attack against RAG systems in which the attacker injects only a single poisoned text, enhancing both feasibility and stealth. Extensive experiments across multiple datasets demonstrate that CorruptRAG achieves higher attack success rates compared to existing baselines.

Do We Really Need to Design New Byzantine-robust Aggregation Rules?

Federated learning (FL) allows multiple clients to collaboratively train a global machine learning model through a server, without exchanging their private training data. However, the decentralized aspect of FL makes it susceptible to poisoning attacks, where malicious clients can manipulate the global model by sending altered local model updates. To counter these attacks, a variety of aggregation rules designed to be resilient to Byzantine failures have been introduced. Nonetheless, these methods can still be vulnerable to sophisticated attacks or depend on unrealistic assumptions about the server. In this paper, we demonstrate that there is no need to design new Byzantine-robust aggregation rules; instead, FL can be secured by enhancing the robustness of well-established aggregation rules. To this end, we present FoundationFL, a novel defense mechanism against poisoning attacks. FoundationFL involves the server generating synthetic updates after receiving local model updates from clients. It then applies existing Byzantine-robust foundational aggregation rules, such as Trimmed-mean or Median, to combine clients' model updates with the synthetic ones. We theoretically establish the convergence performance of FoundationFL under Byzantine settings. Comprehensive experiments across several real-world datasets validate the efficiency of our FoundationFL method.

Poisoning Attacks and Defenses to Federated Unlearning

Federated learning allows multiple clients to collaboratively train a global model with the assistance of a server. However, its distributed nature makes it susceptible to poisoning attacks, where malicious clients can compromise the global model by sending harmful local model updates to the server. To unlearn an accurate global model from a poisoned one after identifying malicious clients, federated unlearning has been introduced. Yet, current research on federated unlearning has primarily concentrated on its effectiveness and efficiency, overlooking the security challenges it presents. In this work, we bridge the gap via proposing BadUnlearn, the first poisoning attacks targeting federated unlearning. In BadUnlearn, malicious clients send specifically designed local model updates to the server during the unlearning process, aiming to ensure that the resulting unlearned model remains poisoned. To mitigate these threats, we propose UnlearnGuard, a robust federated unlearning framework that is provably robust against both existing poisoning attacks and our BadUnlearn. The core concept of UnlearnGuard is for the server to estimate the clients' local model updates during the unlearning process and employ a filtering strategy to verify the accuracy of these estimations. Theoretically, we prove that the model unlearned through UnlearnGuard closely resembles one obtained by train-from-scratch. Empirically, we show that BadUnlearn can effectively corrupt existing federated unlearning methods, while UnlearnGuard remains secure against poisoning attacks.

Byzantine-Robust Federated Learning over Ring-All-Reduce Distributed Computing

Federated learning (FL) has gained attention as a distributed learning paradigm for its data privacy benefits and accelerated convergence through parallel computation. Traditional FL relies on a server-client (SC) architecture, where a central server coordinates multiple clients to train a global model, but this approach faces scalability challenges due to server communication bottlenecks. To overcome this, the ring-all-reduce (RAR) architecture has been introduced, eliminating the central server and achieving bandwidth optimality. However, the tightly coupled nature of RAR's ring topology exposes it to unique Byzantine attack risks not present in SC-based FL. Despite its potential, designing Byzantine-robust RAR-based FL algorithms remains an open problem. To address this gap, we propose BRACE (Byzantine-robust ring-all-reduce), the first RAR-based FL algorithm to achieve both Byzantine robustness and communication efficiency. We provide theoretical guarantees for the convergence of BRACE under Byzantine attacks, demonstrate its bandwidth efficiency, and validate its practical effectiveness through experiments. Our work offers a foundational understanding of Byzantine-robust RAR-based FL design.

Adversarial Attacks to Multi-Modal Models

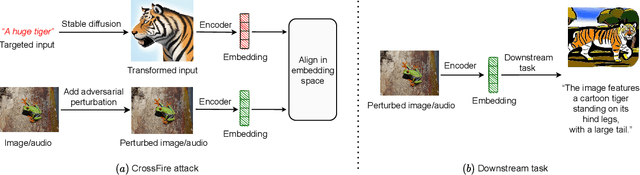
Multi-modal models have gained significant attention due to their powerful capabilities. These models effectively align embeddings across diverse data modalities, showcasing superior performance in downstream tasks compared to their unimodal counterparts. Recent study showed that the attacker can manipulate an image or audio file by altering it in such a way that its embedding matches that of an attacker-chosen targeted input, thereby deceiving downstream models. However, this method often underperforms due to inherent disparities in data from different modalities. In this paper, we introduce CrossFire, an innovative approach to attack multi-modal models. CrossFire begins by transforming the targeted input chosen by the attacker into a format that matches the modality of the original image or audio file. We then formulate our attack as an optimization problem, aiming to minimize the angular deviation between the embeddings of the transformed input and the modified image or audio file. Solving this problem determines the perturbations to be added to the original media. Our extensive experiments on six real-world benchmark datasets reveal that CrossFire can significantly manipulate downstream tasks, surpassing existing attacks. Additionally, we evaluate six defensive strategies against CrossFire, finding that current defenses are insufficient to counteract our CrossFire.

Federated Multi-Objective Learning

In recent years, multi-objective optimization (MOO) emerges as a foundational problem underpinning many multi-agent multi-task learning applications. However, existing algorithms in MOO literature remain limited to centralized learning settings, which do not satisfy the distributed nature and data privacy needs of such multi-agent multi-task learning applications. This motivates us to propose a new federated multi-objective learning (FMOL) framework with multiple clients distributively and collaboratively solving an MOO problem while keeping their training data private. Notably, our FMOL framework allows a different set of objective functions across different clients to support a wide range of applications, which advances and generalizes the MOO formulation to the federated learning paradigm for the first time. For this FMOL framework, we propose two new federated multi-objective optimization (FMOO) algorithms called federated multi-gradient descent averaging (FMGDA) and federated stochastic multi-gradient descent averaging (FSMGDA). Both algorithms allow local updates to significantly reduce communication costs, while achieving the {\em same} convergence rates as those of the their algorithmic counterparts in the single-objective federated learning. Our extensive experiments also corroborate the efficacy of our proposed FMOO algorithms.