PROVEN: Certifying Robustness of Neural Networks with a Probabilistic Approach
Paper and Code
Jan 07, 2019
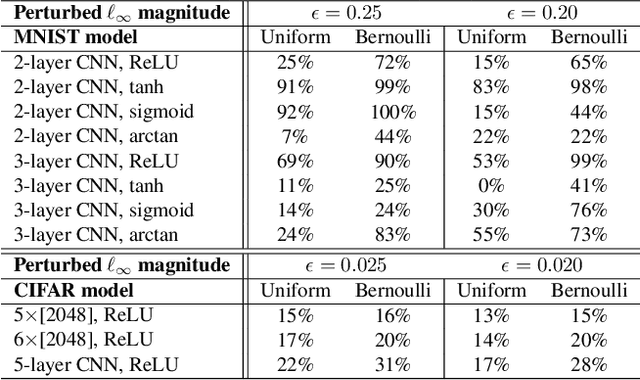
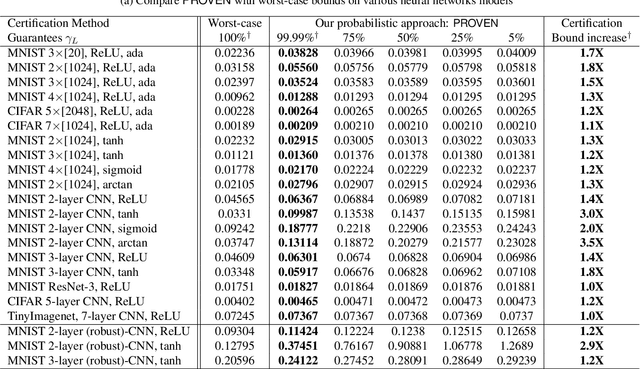
With deep neural networks providing state-of-the-art machine learning models for numerous machine learning tasks, quantifying the robustness of these models has become an important area of research. However, most of the research literature merely focuses on the \textit{worst-case} setting where the input of the neural network is perturbed with noises that are constrained within an $\ell_p$ ball; and several algorithms have been proposed to compute certified lower bounds of minimum adversarial distortion based on such worst-case analysis. In this paper, we address these limitations and extend the approach to a \textit{probabilistic} setting where the additive noises can follow a given distributional characterization. We propose a novel probabilistic framework PROVEN to PRObabilistically VErify Neural networks with statistical guarantees -- i.e., PROVEN certifies the probability that the classifier's top-1 prediction cannot be altered under any constrained $\ell_p$ norm perturbation to a given input. Importantly, we show that it is possible to derive closed-form probabilistic certificates based on current state-of-the-art neural network robustness verification frameworks. Hence, the probabilistic certificates provided by PROVEN come naturally and with almost no overhead when obtaining the worst-case certified lower bounds from existing methods such as Fast-Lin, CROWN and CNN-Cert. Experiments on small and large MNIST and CIFAR neural network models demonstrate our probabilistic approach can achieve up to around $75\%$ improvement in the robustness certification with at least a $99.99\%$ confidence compared with the worst-case robustness certificate delivered by CROWN.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge