A new perspective on low-rank optimization
Paper and Code
May 12, 2021
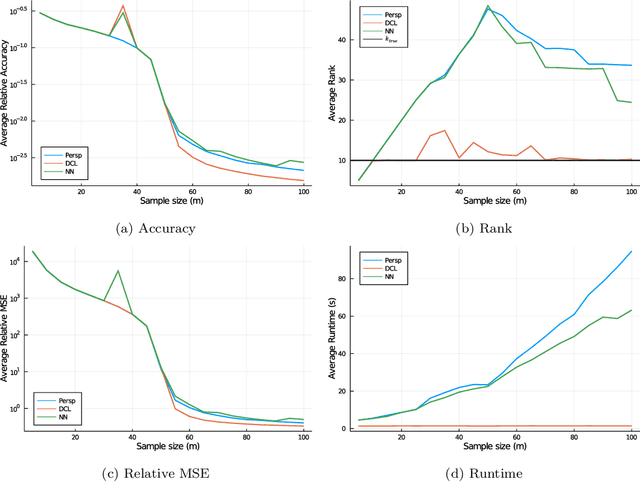

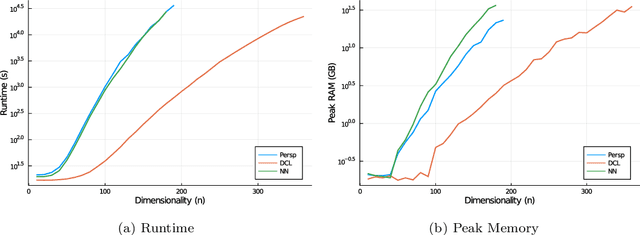
A key question in many low-rank problems throughout optimization, machine learning, and statistics is to characterize the convex hulls of simple low-rank sets and judiciously apply these convex hulls to obtain strong yet computationally tractable convex relaxations. We invoke the matrix perspective function - the matrix analog of the perspective function-and characterize explicitly the convex hull of epigraphs of convex quadratic, matrix exponential, and matrix power functions under low-rank constraints. Further, we exploit these characterizations to develop strong relaxations for a variety of low-rank problems including reduced rank regression, non-negative matrix factorization, and factor analysis. We establish that these relaxations can be modeled via semidefinite and matrix power cone constraints, and thus optimized over tractably. The proposed approach parallels and generalizes the perspective reformulation technique in mixed-integer optimization, and leads to new relaxations for a broad class of problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge