Sparse PCA With Multiple Components
Paper and Code
Sep 29, 2022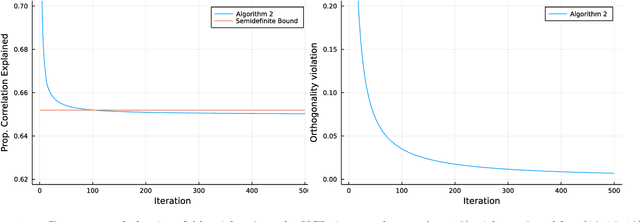
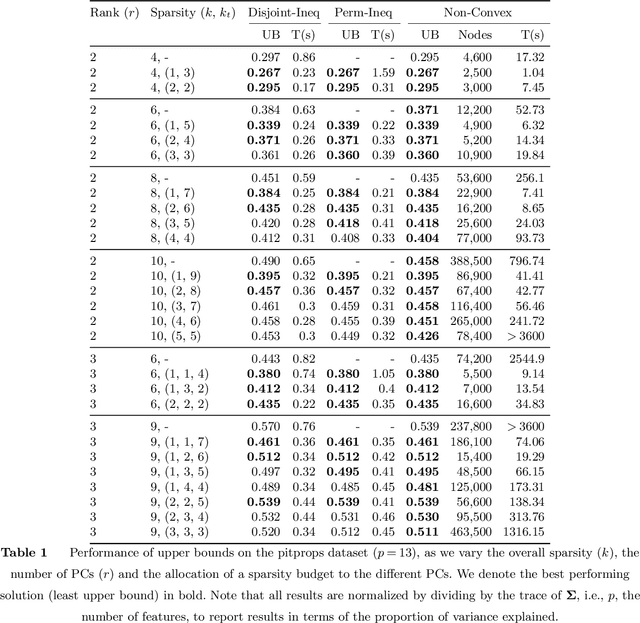
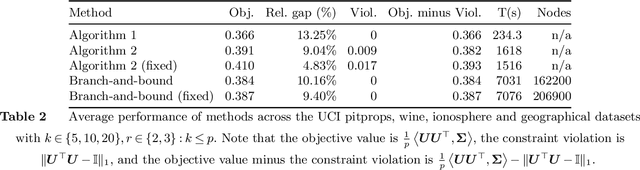
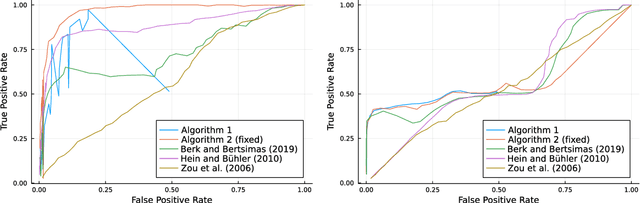
Sparse Principal Component Analysis is a cardinal technique for obtaining combinations of features, or principal components (PCs), that explain the variance of high-dimensional datasets in an interpretable manner. At its heart, this involves solving a sparsity and orthogonality constrained convex maximization problem, which is extremely computationally challenging. Most existing work address sparse PCA via heuristics such as iteratively computing one sparse PC and deflating the covariance matrix, which does not guarantee the orthogonality, let alone the optimality, of the resulting solution. We challenge this status by reformulating the orthogonality conditions as rank constraints and optimizing over the sparsity and rank constraints simultaneously. We design tight semidefinite relaxations and propose tractable second-order cone versions of these relaxations which supply high-quality upper bounds. We also design valid second-order cone inequalities which hold when each PC's individual sparsity is specified, and demonstrate that these inequalities tighten our relaxations significantly. Moreover, we propose exact methods and rounding mechanisms that exploit these relaxations' tightness to obtain solutions with a bound gap on the order of 1%-5% for real-world datasets with p = 100s or 1000s of features and r \in {2, 3} components. We investigate the performance of our methods in spiked covariance settings and demonstrate that simultaneously considering the orthogonality and sparsity constraints leads to improvements in the Area Under the ROC curve of 2%-8% compared to state-of-the-art deflation methods. All in all, our approach solves sparse PCA problems with multiple components to certifiable (near) optimality in a practically tractable fashion.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge