Predictive Low Rank Matrix Learning under Partial Observations: Mixed-Projection ADMM

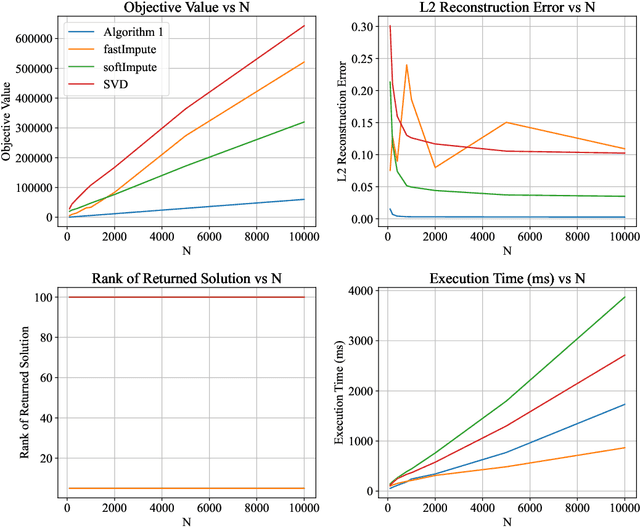
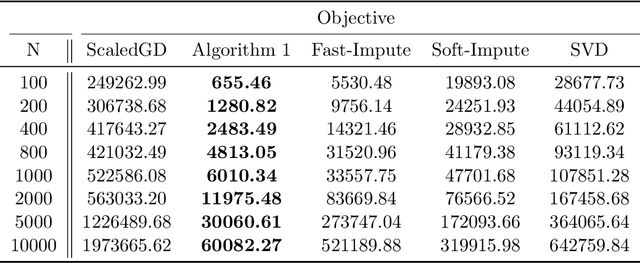
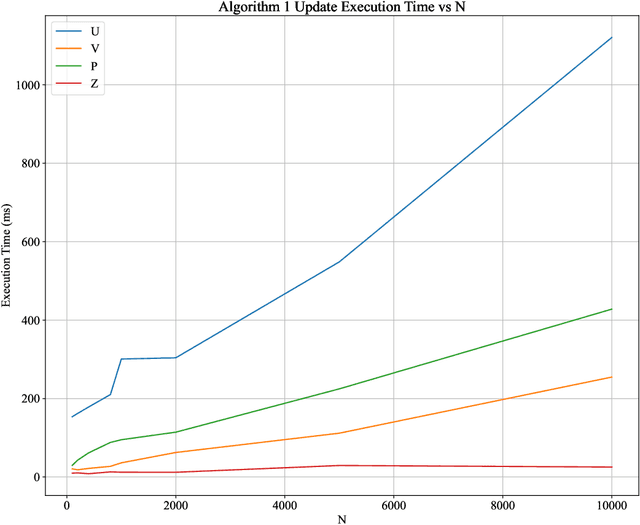
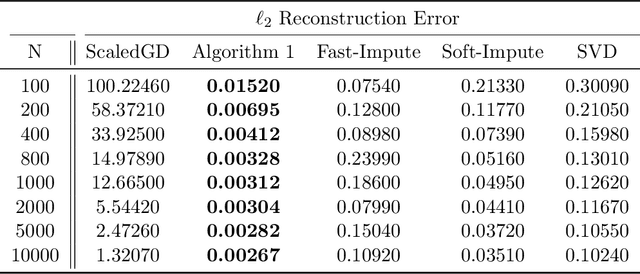
We study the problem of learning a partially observed matrix under the low rank assumption in the presence of fully observed side information that depends linearly on the true underlying matrix. This problem consists of an important generalization of the Matrix Completion problem, a central problem in Statistics, Operations Research and Machine Learning, that arises in applications such as recommendation systems, signal processing, system identification and image denoising. We formalize this problem as an optimization problem with an objective that balances the strength of the fit of the reconstruction to the observed entries with the ability of the reconstruction to be predictive of the side information. We derive a mixed-projection reformulation of the resulting optimization problem and present a strong semidefinite cone relaxation. We design an efficient, scalable alternating direction method of multipliers algorithm that produces high quality feasible solutions to the problem of interest. Our numerical results demonstrate that in the small rank regime ($k \leq 15$), our algorithm outputs solutions that achieve on average $79\%$ lower objective value and $90.1\%$ lower $\ell_2$ reconstruction error than the solutions returned by the experiment-wise best performing benchmark method. The runtime of our algorithm is competitive with and often superior to that of the benchmark methods. Our algorithm is able to solve problems with $n = 10000$ rows and $m = 10000$ columns in less than a minute.

Sparse Plus Low Rank Matrix Decomposition: A Discrete Optimization Approach

We study the Sparse Plus Low Rank decomposition problem (SLR), which is the problem of decomposing a corrupted data matrix $\mathbf{D}$ into a sparse matrix $\mathbf{Y}$ containing the perturbations plus a low rank matrix $\mathbf{X}$. SLR is a fundamental problem in Operations Research and Machine Learning arising in many applications such as data compression, latent semantic indexing, collaborative filtering and medical imaging. We introduce a novel formulation for SLR that directly models the underlying discreteness of the problem. For this formulation, we develop an alternating minimization heuristic to compute high quality solutions and a novel semidefinite relaxation that provides meaningful bounds for the solutions returned by our heuristic. We further develop a custom branch and bound routine that leverages our heuristic and convex relaxation that solves small instances of SLR to certifiable near-optimality. Our heuristic can scale to $n=10000$ in hours, our relaxation can scale to $n=200$ in hours, and our branch and bound algorithm can scale to $n=25$ in minutes. Our numerical results demonstrate that our approach outperforms existing state-of-the-art approaches in terms of the MSE of the low rank matrix and that of the sparse matrix.