Solving optimization problems with Blackwell approachability
Paper and Code
Feb 24, 2022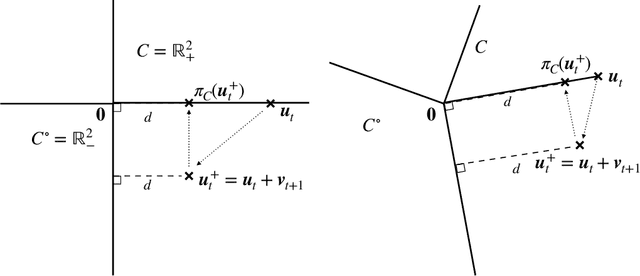
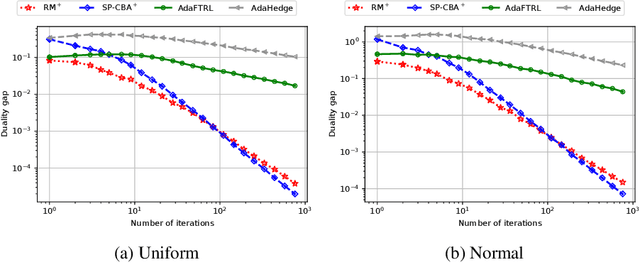
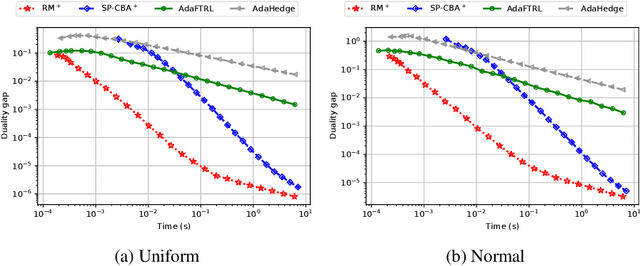
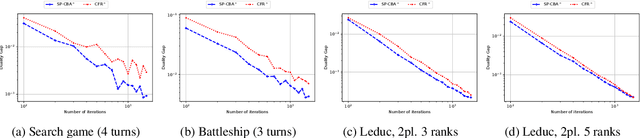
We introduce the Conic Blackwell Algorithm$^+$ (CBA$^+$) regret minimizer, a new parameter- and scale-free regret minimizer for general convex sets. CBA$^+$ is based on Blackwell approachability and attains $O(\sqrt{T})$ regret. We show how to efficiently instantiate CBA$^+$ for many decision sets of interest, including the simplex, $\ell_{p}$ norm balls, and ellipsoidal confidence regions in the simplex. Based on CBA$^+$, we introduce SP-CBA$^+$, a new parameter-free algorithm for solving convex-concave saddle-point problems, which achieves a $O(1/\sqrt{T})$ ergodic rate of convergence. In our simulations, we demonstrate the wide applicability of SP-CBA$^+$ on several standard saddle-point problems, including matrix games, extensive-form games, distributionally robust logistic regression, and Markov decision processes. In each setting, SP-CBA$^+$ achieves state-of-the-art numerical performance, and outperforms classical methods, without the need for any choice of step sizes or other algorithmic parameters.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge