Large-Scale Contextual Market Equilibrium Computation through Deep Learning

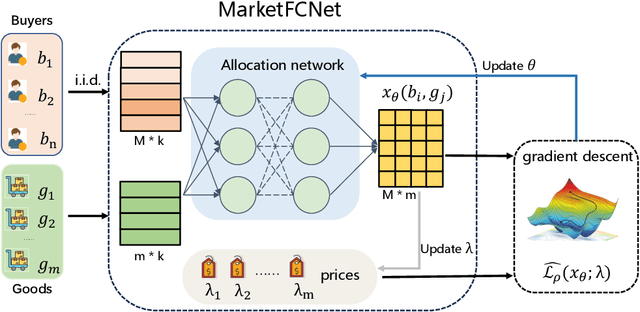
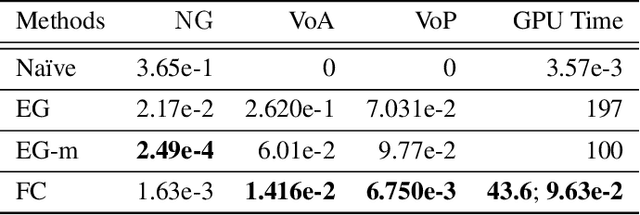
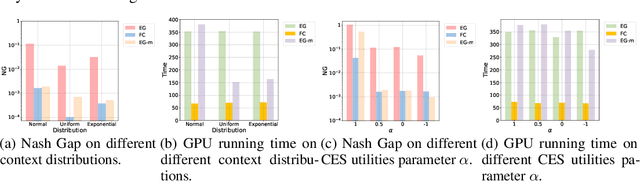
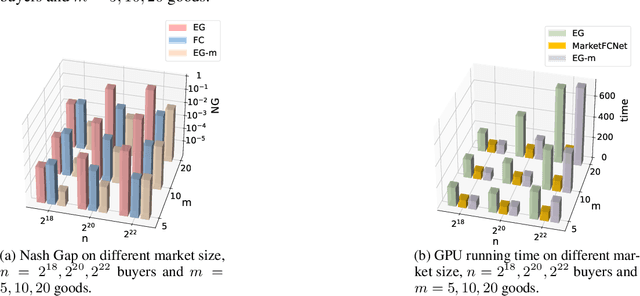
Market equilibrium is one of the most fundamental solution concepts in economics and social optimization analysis. Existing works on market equilibrium computation primarily focus on settings with a relatively small number of buyers. Motivated by this, our paper investigates the computation of market equilibrium in scenarios with a large-scale buyer population, where buyers and goods are represented by their contexts. Building on this realistic and generalized contextual market model, we introduce MarketFCNet, a deep learning-based method for approximating market equilibrium. We start by parameterizing the allocation of each good to each buyer using a neural network, which depends solely on the context of the buyer and the good. Next, we propose an efficient method to estimate the loss function of the training algorithm unbiasedly, enabling us to optimize the network parameters through gradient descent. To evaluate the approximated solution, we introduce a metric called Nash Gap, which quantifies the deviation of the given allocation and price pair from the market equilibrium. Experimental results indicate that MarketFCNet delivers competitive performance and significantly lower running times compared to existing methods as the market scale expands, demonstrating the potential of deep learning-based methods to accelerate the approximation of large-scale contextual market equilibrium.

Are Equivariant Equilibrium Approximators Beneficial?

Recently, remarkable progress has been made by approximating Nash equilibrium (NE), correlated equilibrium (CE), and coarse correlated equilibrium (CCE) through function approximation that trains a neural network to predict equilibria from game representations. Furthermore, equivariant architectures are widely adopted in designing such equilibrium approximators in normal-form games. In this paper, we theoretically characterize benefits and limitations of equivariant equilibrium approximators. For the benefits, we show that they enjoy better generalizability than general ones and can achieve better approximations when the payoff distribution is permutation-invariant. For the limitations, we discuss their drawbacks in terms of equilibrium selection and social welfare. Together, our results help to understand the role of equivariance in equilibrium approximators.