Are Bounded Contracts Learnable and Approximately Optimal?
Paper and Code
Feb 22, 2024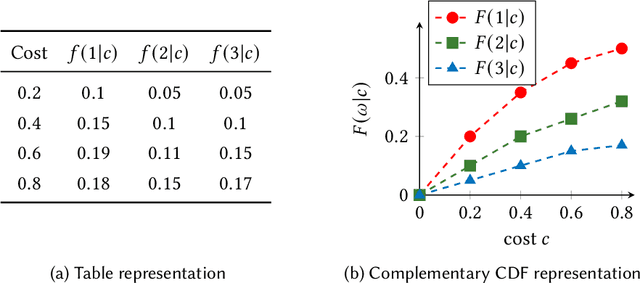

This paper considers the hidden-action model of the principal-agent problem, in which a principal incentivizes an agent to work on a project using a contract. We investigate whether contracts with bounded payments are learnable and approximately optimal. Our main results are two learning algorithms that can find a nearly optimal bounded contract using a polynomial number of queries, under two standard assumptions in the literature: a costlier action for the agent leads to a better outcome distribution for the principal, and the agent's cost/effort has diminishing returns. Our polynomial query complexity upper bound shows that standard assumptions are sufficient for achieving an exponential improvement upon the known lower bound for general instances. Unlike the existing algorithms, which relied on discretizing the contract space, our algorithms directly learn the underlying outcome distributions. As for the approximate optimality of bounded contracts, we find that they could be far from optimal in terms of multiplicative or additive approximation, but satisfy a notion of mixed approximation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge