Are Bounded Contracts Learnable and Approximately Optimal?

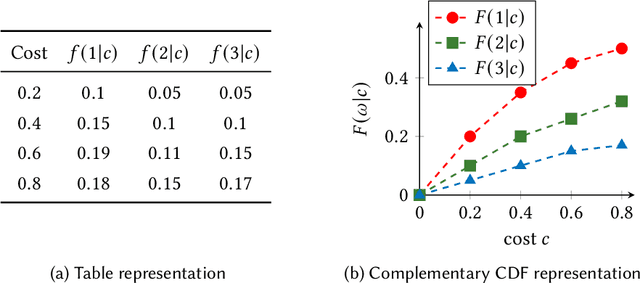
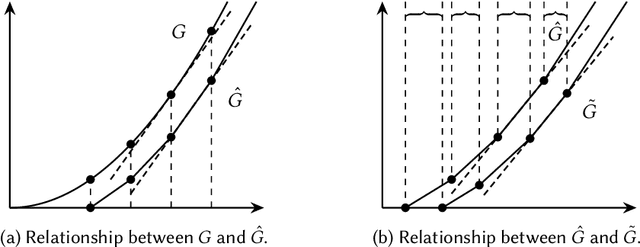
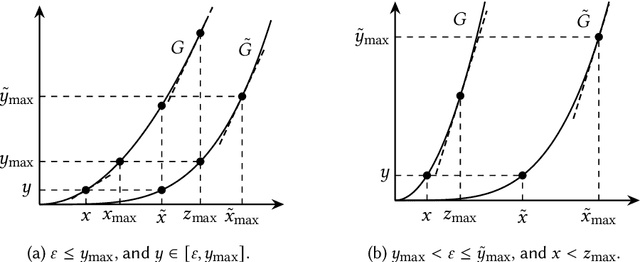
This paper considers the hidden-action model of the principal-agent problem, in which a principal incentivizes an agent to work on a project using a contract. We investigate whether contracts with bounded payments are learnable and approximately optimal. Our main results are two learning algorithms that can find a nearly optimal bounded contract using a polynomial number of queries, under two standard assumptions in the literature: a costlier action for the agent leads to a better outcome distribution for the principal, and the agent's cost/effort has diminishing returns. Our polynomial query complexity upper bound shows that standard assumptions are sufficient for achieving an exponential improvement upon the known lower bound for general instances. Unlike the existing algorithms, which relied on discretizing the contract space, our algorithms directly learn the underlying outcome distributions. As for the approximate optimality of bounded contracts, we find that they could be far from optimal in terms of multiplicative or additive approximation, but satisfy a notion of mixed approximation.

Robust Decision Aggregation with Second-order Information

We consider a decision aggregation problem with two experts who each make a binary recommendation after observing a private signal about an unknown binary world state. An agent, who does not know the joint information structure between signals and states, sees the experts' recommendations and aims to match the action with the true state. Under the scenario, we study whether supplemented additionally with second-order information (each expert's forecast on the other's recommendation) could enable a better aggregation. We adopt a minimax regret framework to evaluate the aggregator's performance, by comparing it to an omniscient benchmark that knows the joint information structure. With general information structures, we show that second-order information provides no benefit. No aggregator can improve over a trivial aggregator, which always follows the first expert's recommendation. However, positive results emerge when we assume experts' signals are conditionally independent given the world state. When the aggregator is deterministic, we present a robust aggregator that leverages second-order information, which can significantly outperform counterparts without it. Second, when two experts are homogeneous, by adding a non-degenerate assumption on the signals, we demonstrate that random aggregators using second-order information can surpass optimal ones without it. In the remaining settings, the second-order information is not beneficial. We also extend the above results to the setting when the aggregator's utility function is more general.

Coordinated Dynamic Bidding in Repeated Second-Price Auctions with Budgets

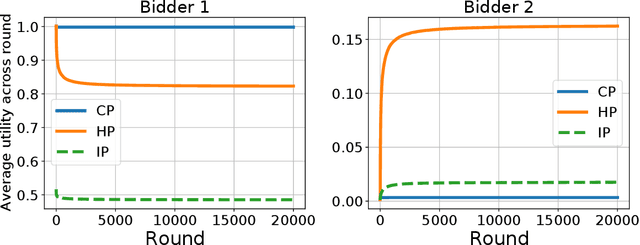
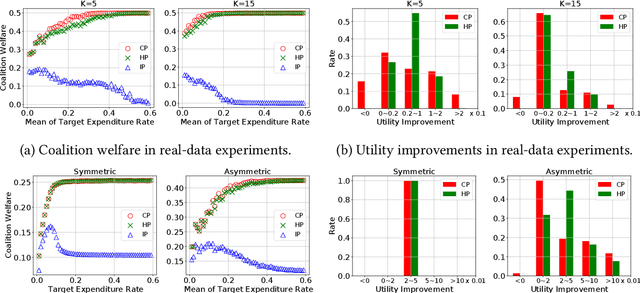
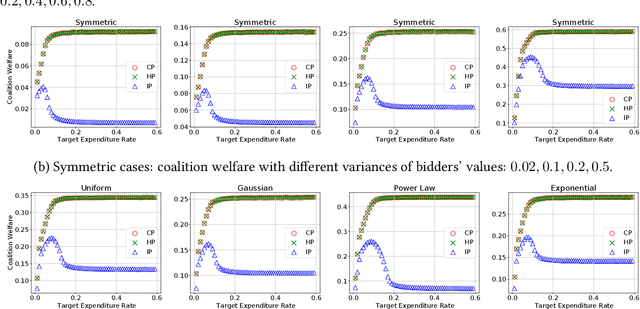
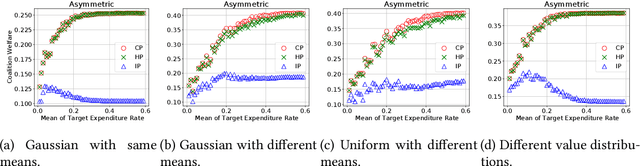
In online ad markets, a rising number of advertisers are employing bidding agencies to participate in ad auctions. These agencies are specialized in designing online algorithms and bidding on behalf of their clients. Typically, an agency usually has information on multiple advertisers, so she can potentially coordinate bids to help her clients achieve higher utilities than those under independent bidding. In this paper, we study coordinated online bidding algorithms in repeated second-price auctions with budgets. We propose algorithms that guarantee every client a higher utility than the best she can get under independent bidding. We show that these algorithms achieve maximal coalition welfare and discuss bidders' incentives to misreport their budgets, in symmetric cases. Our proofs combine the techniques of online learning and equilibrium analysis, overcoming the difficulty of competing with a multi-dimensional benchmark. The performance of our algorithms is further evaluated by experiments on both synthetic and real data. To the best of our knowledge, we are the first to consider bidder coordination in online repeated auctions with constraints.

On the Re-Solving Heuristic for Contextual Bandits with Knapsacks

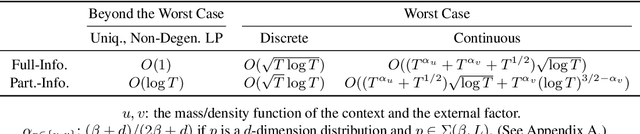
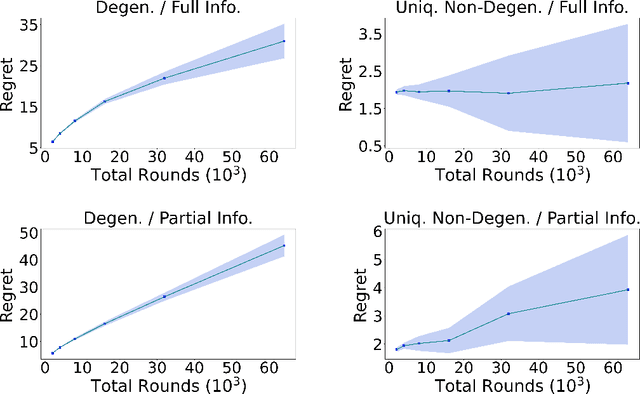
In the problem of (binary) contextual bandits with knapsacks (CBwK), the agent receives an i.i.d. context in each of the $T$ rounds and chooses an action, resulting in a random reward and a random consumption of resources that are related to an i.i.d. external factor. The agent's goal is to maximize the accumulated reward under the initial resource constraints. In this work, we combine the re-solving heuristic, which proved successful in revenue management, with distribution estimation techniques to solve this problem. We consider two different information feedback models, with full and partial information, which vary in the difficulty of getting a sample of the external factor. Under both information feedback settings, we achieve two-way results: (1) For general problems, we show that our algorithm gets an $\widetilde O(T^{\alpha_u} + T^{\alpha_v} + T^{1/2})$ regret against the fluid benchmark. Here, $\alpha_u$ and $\alpha_v$ reflect the complexity of the context and external factor distributions, respectively. This result is comparable to existing results. (2) When the fluid problem is linear programming with a unique and non-degenerate optimal solution, our algorithm leads to an $\widetilde O(1)$ regret. To the best of our knowledge, this is the first $\widetilde O(1)$ regret result in the CBwK problem regardless of information feedback models. We further use numerical experiments to verify our results.

Dynamic Budget Throttling in Repeated Second-Price Auctions

Throttling is one of the most popular budget control methods in today's online advertising markets. When a budget-constrained advertiser employs throttling, she can choose whether or not to participate in an auction after the advertising platform recommends a bid. This paper focuses on the dynamic budget throttling process in repeated second-price auctions from a theoretical view. An essential feature of the underlying problem is that the advertiser does not know the distribution of the highest competing bid upon entering the market. To model the difficulty of eliminating such uncertainty, we consider two different information structures. The advertiser could obtain the highest competing bid in each round with full-information feedback. Meanwhile, with partial information feedback, the advertiser could only have access to the highest competing bid in the auctions she participates in. We propose the OGD-CB algorithm, which involves simultaneous distribution learning and revenue optimization. In both settings, we demonstrate that this algorithm guarantees an $O(\sqrt{T\log T})$ regret with probability $1 - O(1/T)$ relative to the fluid adaptive throttling benchmark. By proving a lower bound of $\Omega(\sqrt{T})$ on the minimal regret for even the hindsight optimum, we establish the near optimality of our algorithm. Finally, we compare the fluid optimum of throttling to that of pacing, another widely adopted budget control method. The numerical relationship of these benchmarks sheds new light on the understanding of different online algorithms for revenue maximization under budget constraints.