CIS-BA: Continuous Interaction Space Based Backdoor Attack for Object Detection in the Real-World

Object detection models deployed in real-world applications such as autonomous driving face serious threats from backdoor attacks. Despite their practical effectiveness,existing methods are inherently limited in both capability and robustness due to their dependence on single-trigger-single-object mappings and fragile pixel-level cues. We propose CIS-BA, a novel backdoor attack paradigm that redefines trigger design by shifting from static object features to continuous inter-object interaction patterns that describe how objects co-occur and interact in a scene. By modeling these patterns as a continuous interaction space, CIS-BA introduces space triggers that, for the first time, enable a multi-trigger-multi-object attack mechanism while achieving robustness through invariant geometric relations. To implement this paradigm, we design CIS-Frame, which constructs space triggers via interaction analysis, formalizes them as class-geometry constraints for sample poisoning, and embeds the backdoor during detector training. CIS-Frame supports both single-object attacks (object misclassification and disappearance) and multi-object simultaneous attacks, enabling complex and coordinated effects across diverse interaction states. Experiments on MS-COCO and real-world videos show that CIS-BA achieves over 97% attack success under complex environments and maintains over 95% effectiveness under dynamic multi-trigger conditions, while evading three state-of-the-art defenses. In summary, CIS-BA extends the landscape of backdoor attacks in interaction-intensive scenarios and provides new insights into the security of object detection systems.

RefLoRA: Refactored Low-Rank Adaptation for Efficient Fine-Tuning of Large Models

Low-Rank Adaptation (LoRA) lowers the computational and memory overhead of fine-tuning large models by updating a low-dimensional subspace of the pre-trained weight matrix. Albeit efficient, LoRA exhibits suboptimal convergence and noticeable performance degradation, due to inconsistent and imbalanced weight updates induced by its nonunique low-rank factorizations. To overcome these limitations, this article identifies the optimal low-rank factorization per step that minimizes an upper bound on the loss. The resultant refactored low-rank adaptation (RefLoRA) method promotes a flatter loss landscape, along with consistent and balanced weight updates, thus speeding up stable convergence. Extensive experiments evaluate RefLoRA on natural language understanding, and commonsense reasoning tasks with popular large language models including DeBERTaV3, LLaMA-7B, LLaMA2-7B and LLaMA3-8B. The numerical tests corroborate that RefLoRA converges faster, outperforms various benchmarks, and enjoys negligible computational overhead compared to state-of-the-art LoRA variants.

Preconditioned Sharpness-Aware Minimization: Unifying Analysis and a Novel Learning Algorithm

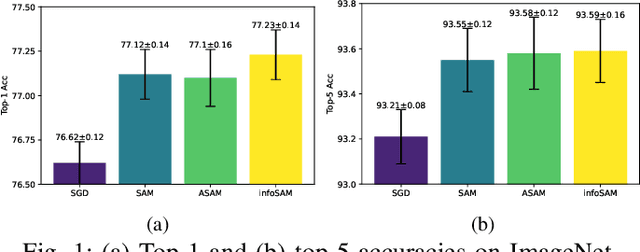
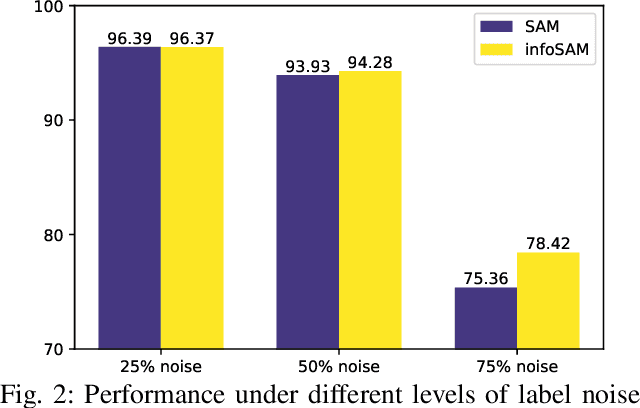
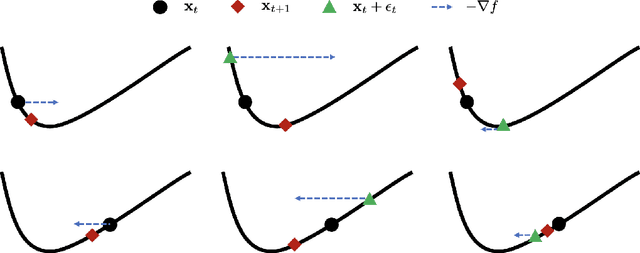
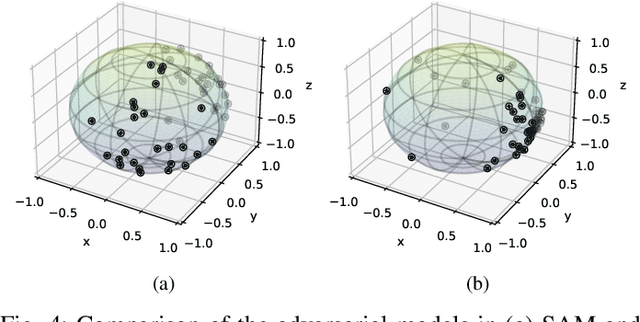
Targeting solutions over `flat' regions of the loss landscape, sharpness-aware minimization (SAM) has emerged as a powerful tool to improve generalizability of deep neural network based learning. While several SAM variants have been developed to this end, a unifying approach that also guides principled algorithm design has been elusive. This contribution leverages preconditioning (pre) to unify SAM variants and provide not only unifying convergence analysis, but also valuable insights. Building upon preSAM, a novel algorithm termed infoSAM is introduced to address the so-called adversarial model degradation issue in SAM by adjusting gradients depending on noise estimates. Extensive numerical tests demonstrate the superiority of infoSAM across various benchmarks.

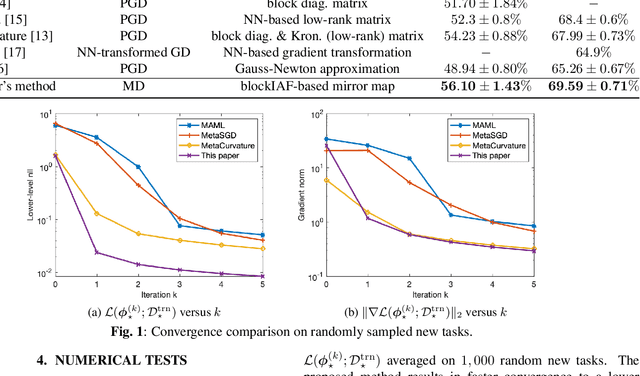
Meta-Learning with Versatile Loss Geometries for Fast Adaptation Using Mirror Descent

Utilizing task-invariant prior knowledge extracted from related tasks, meta-learning is a principled framework that empowers learning a new task especially when data records are limited. A fundamental challenge in meta-learning is how to quickly "adapt" the extracted prior in order to train a task-specific model within a few optimization steps. Existing approaches deal with this challenge using a preconditioner that enhances convergence of the per-task training process. Though effective in representing locally a quadratic training loss, these simple linear preconditioners can hardly capture complex loss geometries. The present contribution addresses this limitation by learning a nonlinear mirror map, which induces a versatile distance metric to enable capturing and optimizing a wide range of loss geometries, hence facilitating the per-task training. Numerical tests on few-shot learning datasets demonstrate the superior expressiveness and convergence of the advocated approach.

Scalable Bayesian Meta-Learning through Generalized Implicit Gradients

Meta-learning owns unique effectiveness and swiftness in tackling emerging tasks with limited data. Its broad applicability is revealed by viewing it as a bi-level optimization problem. The resultant algorithmic viewpoint however, faces scalability issues when the inner-level optimization relies on gradient-based iterations. Implicit differentiation has been considered to alleviate this challenge, but it is restricted to an isotropic Gaussian prior, and only favors deterministic meta-learning approaches. This work markedly mitigates the scalability bottleneck by cross-fertilizing the benefits of implicit differentiation to probabilistic Bayesian meta-learning. The novel implicit Bayesian meta-learning (iBaML) method not only broadens the scope of learnable priors, but also quantifies the associated uncertainty. Furthermore, the ultimate complexity is well controlled regardless of the inner-level optimization trajectory. Analytical error bounds are established to demonstrate the precision and efficiency of the generalized implicit gradient over the explicit one. Extensive numerical tests are also carried out to empirically validate the performance of the proposed method.

Dense Color Constancy with Effective Edge Augmentation

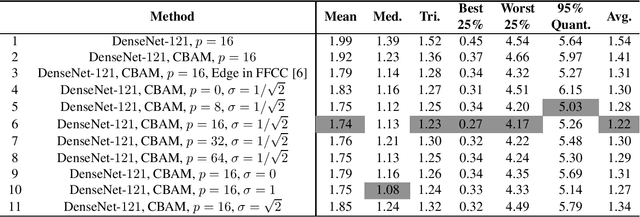
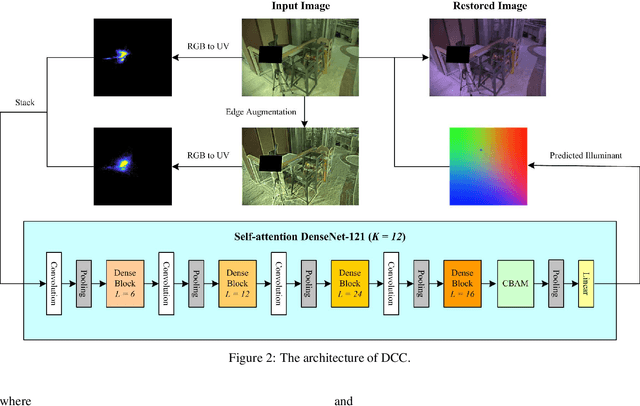
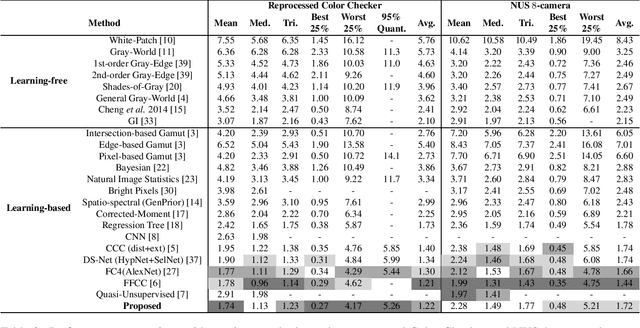
Recently, computational color constancy via convolutional neural networks (CNNs) has received much attention. In this paper, we propose a color constancy algorithm called the Dense Color Constancy (DCC), which employs a self-attention DenseNet to estimate the illuminant based on the $2$D $\log$-chrominance histograms of input images and their augmented edges. The augmented edges help to tell apart the edge and non-edge pixels in the $\log$-histogram, which largely contribute to the feature extraction and color ambiguity elimination, thereby improving the accuracy of illuminant estimation. Experiments on benchmark datasets show that the DCC algorithm is very effective for illuminant estimation compared to the state-of-the-art methods.