Zheng Wei
NQKV: A KV Cache Quantization Scheme Based on Normal Distribution Characteristics
May 22, 2025Abstract:Large Language Models (LLMs) have demonstrated remarkable proficiency across a wide range of tasks. However, LLMs often require larger batch sizes to enhance throughput or longer context lengths to meet task demands, which significantly increases the memory resource consumption of the Key-Value (KV) cache during inference, becoming a major bottleneck in LLM deployment. To address this issue, quantization is a common and straightforward approach. Currently, quantization methods for activations are limited to 8-bit, and quantization to even lower bits can lead to substantial accuracy drops. To further save space by quantizing the KV cache to even lower bits, we analyzed the element distribution of the KV cache and designed the NQKV algorithm. Since the elements within each block of the KV cache follow a normal distribution, NQKV employs per-block quantile quantization to achieve information-theoretically optimal quantization error. Without significantly compromising model output quality, NQKV enables the OPT model to perform inference with an 2x larger batch size or a 4x longer context length, and it improves throughput by 9.3x compared to when the KV cache is not used.
Generative AI for Film Creation: A Survey of Recent Advances
Apr 11, 2025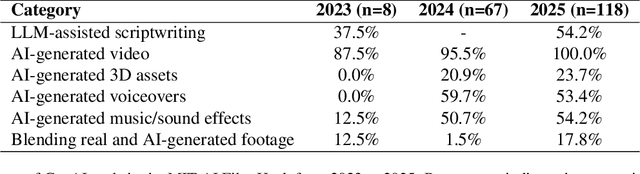


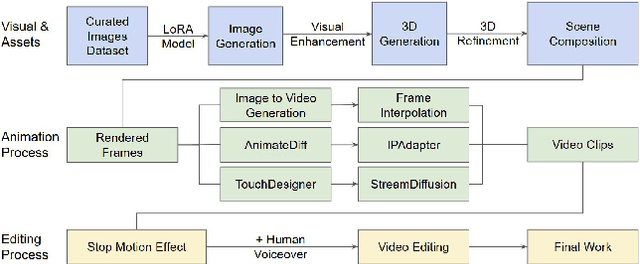
Abstract:Generative AI (GenAI) is transforming filmmaking, equipping artists with tools like text-to-image and image-to-video diffusion, neural radiance fields, avatar generation, and 3D synthesis. This paper examines the adoption of these technologies in filmmaking, analyzing workflows from recent AI-driven films to understand how GenAI contributes to character creation, aesthetic styling, and narration. We explore key strategies for maintaining character consistency, achieving stylistic coherence, and ensuring motion continuity. Additionally, we highlight emerging trends such as the growing use of 3D generation and the integration of real footage with AI-generated elements. Beyond technical advancements, we examine how GenAI is enabling new artistic expressions, from generating hard-to-shoot footage to dreamlike diffusion-based morphing effects, abstract visuals, and unworldly objects. We also gather artists' feedback on challenges and desired improvements, including consistency, controllability, fine-grained editing, and motion refinement. Our study provides insights into the evolving intersection of AI and filmmaking, offering a roadmap for researchers and artists navigating this rapidly expanding field.
Feature Selection Based on Orthogonal Constraints and Polygon Area
Feb 25, 2024Abstract:The goal of feature selection is to choose the optimal subset of features for a recognition task by evaluating the importance of each feature, thereby achieving effective dimensionality reduction. Currently, proposed feature selection methods often overlook the discriminative dependencies between features and labels. To address this problem, this paper introduces a novel orthogonal regression model incorporating the area of a polygon. The model can intuitively capture the discriminative dependencies between features and labels. Additionally, this paper employs a hybrid non-monotone linear search method to efficiently tackle the non-convex optimization challenge posed by orthogonal constraints. Experimental results demonstrate that our approach not only effectively captures discriminative dependency information but also surpasses traditional methods in reducing feature dimensions and enhancing classification performance.
Hetero$^2$Net: Heterophily-aware Representation Learning on Heterogenerous Graphs
Oct 18, 2023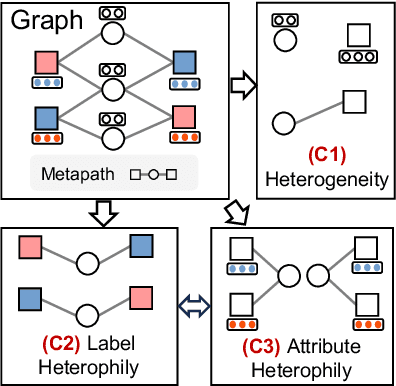
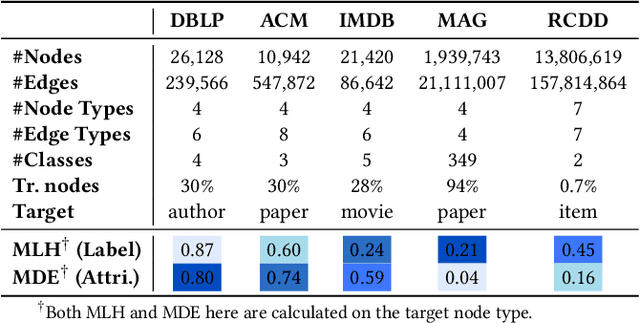
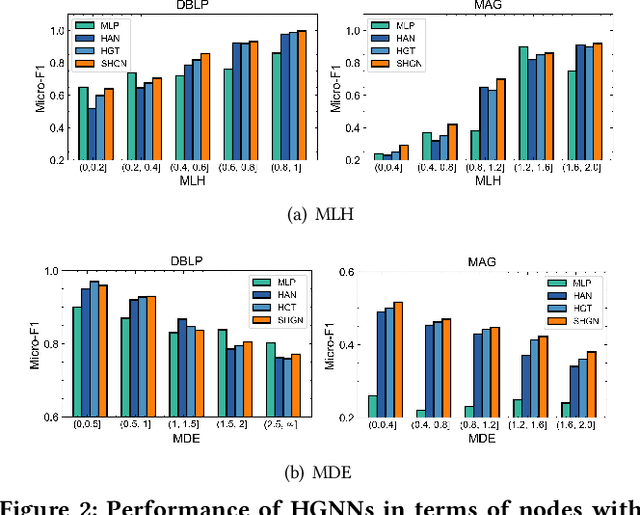
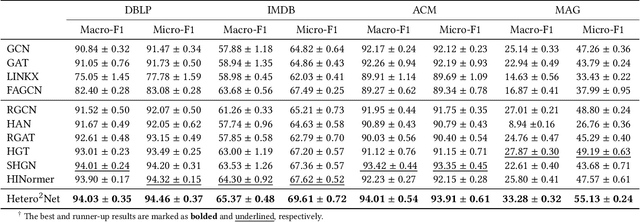
Abstract:Real-world graphs are typically complex, exhibiting heterogeneity in the global structure, as well as strong heterophily within local neighborhoods. While a growing body of literature has revealed the limitations of common graph neural networks (GNNs) in handling homogeneous graphs with heterophily, little work has been conducted on investigating the heterophily properties in the context of heterogeneous graphs. To bridge this research gap, we identify the heterophily in heterogeneous graphs using metapaths and propose two practical metrics to quantitatively describe the levels of heterophily. Through in-depth investigations on several real-world heterogeneous graphs exhibiting varying levels of heterophily, we have observed that heterogeneous graph neural networks (HGNNs), which inherit many mechanisms from GNNs designed for homogeneous graphs, fail to generalize to heterogeneous graphs with heterophily or low level of homophily. To address the challenge, we present Hetero$^2$Net, a heterophily-aware HGNN that incorporates both masked metapath prediction and masked label prediction tasks to effectively and flexibly handle both homophilic and heterophilic heterogeneous graphs. We evaluate the performance of Hetero$^2$Net on five real-world heterogeneous graph benchmarks with varying levels of heterophily. The results demonstrate that Hetero$^2$Net outperforms strong baselines in the semi-supervised node classification task, providing valuable insights into effectively handling more complex heterogeneous graphs.
Fast Graph Subset Selection Based on G-optimal Design
Dec 31, 2021



Abstract:Graph sampling theory extends the traditional sampling theory to graphs with topological structures. As a key part of the graph sampling theory, subset selection chooses nodes on graphs as samples to reconstruct the original signal. Due to the eigen-decomposition operation for Laplacian matrices of graphs, however, existing subset selection methods usually require high-complexity calculations. In this paper, with an aim of enhancing the computational efficiency of subset selection on graphs, we propose a novel objective function based on the optimal experimental design. Theoretical analysis shows that this function enjoys an $\alpha$-supermodular property with a provable lower bound on $\alpha$. The objective function, together with an approximate of the low-pass filter on graphs, suggests a fast subset selection method that does not require any eigen-decomposition operation. Experimental results show that the proposed method exhibits high computational efficiency, while having competitive results compared to the state-of-the-art ones, especially when the sampling rate is low.
Applying Differential Privacy to Tensor Completion
Oct 13, 2021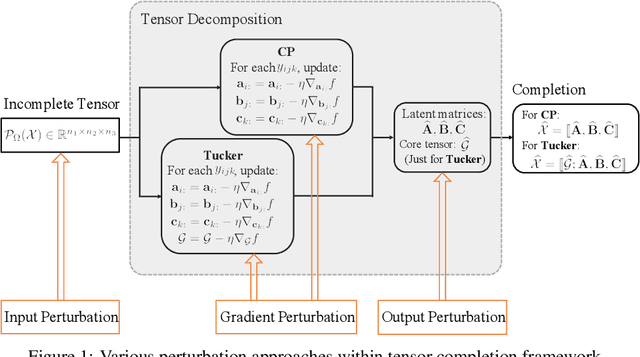
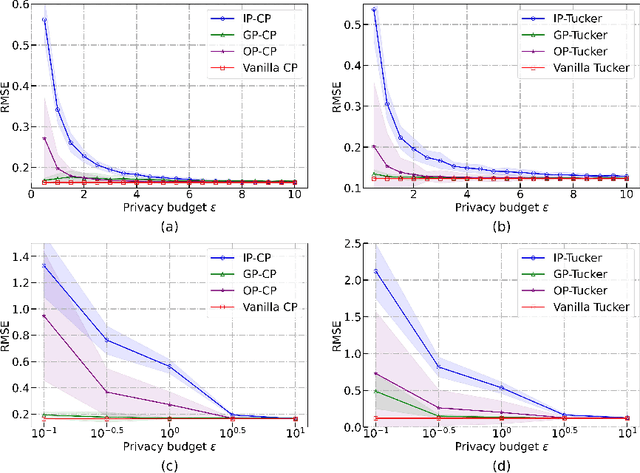
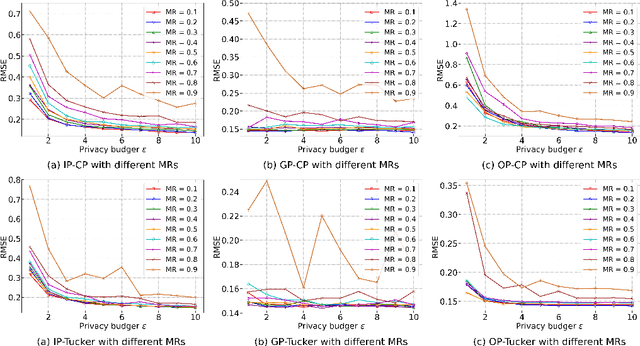
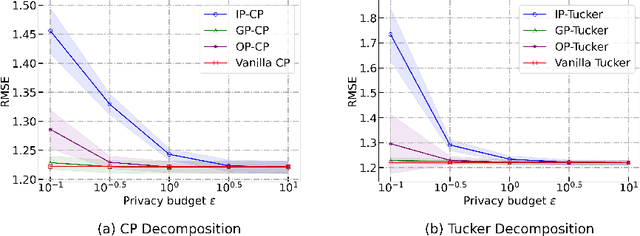
Abstract:Tensor completion aims at filling the missing or unobserved entries based on partially observed tensors. However, utilization of the observed tensors often raises serious privacy concerns in many practical scenarios. To address this issue, we propose a solid and unified framework that contains several approaches for applying differential privacy to the two most widely used tensor decomposition methods: i) CANDECOMP/PARAFAC~(CP) and ii) Tucker decompositions. For each approach, we establish a rigorous privacy guarantee and meanwhile evaluate the privacy-accuracy trade-off. Experiments on synthetic and real-world datasets demonstrate that our proposal achieves high accuracy for tensor completion while ensuring strong privacy protections.
SAM: A Self-adaptive Attention Module for Context-Aware Recommendation System
Oct 13, 2021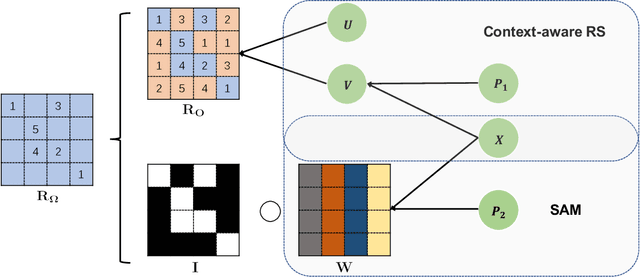
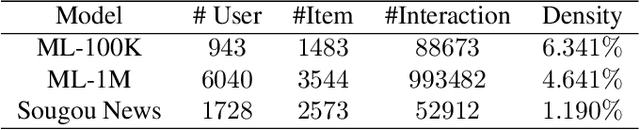
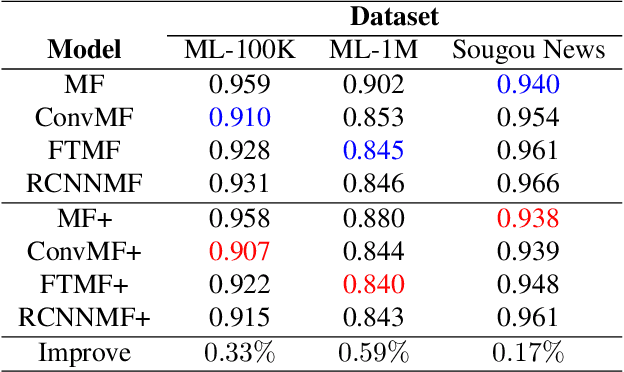
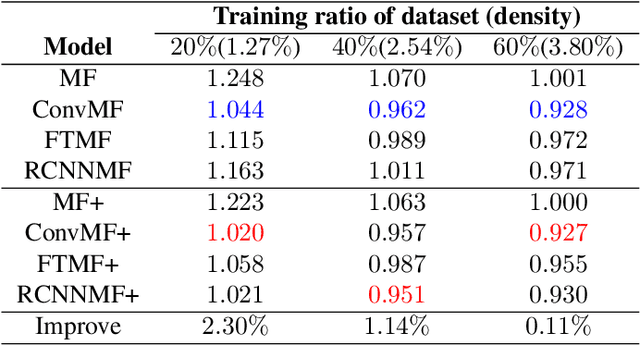
Abstract:Recently, textual information has been proved to play a positive role in recommendation systems. However, most of the existing methods only focus on representation learning of textual information in ratings, while potential selection bias induced by the textual information is ignored. In this work, we propose a novel and general self-adaptive module, the Self-adaptive Attention Module (SAM), which adjusts the selection bias by capturing contextual information based on its representation. This module can be embedded into recommendation systems that contain learning components of contextual information. Experimental results on three real-world datasets demonstrate the effectiveness of our proposal, and the state-of-the-art models with SAM significantly outperform the original ones.
One-Bit Matrix Completion with Differential Privacy
Oct 11, 2021



Abstract:Matrix completion is a prevailing collaborative filtering method for recommendation systems that requires the data offered by users to provide personalized service. However, due to insidious attacks and unexpected inference, the release of user data often raises serious privacy concerns. Most of the existing solutions focus on improving the privacy guarantee for general matrix completion. As a special case, in recommendation systems where the observations are binary, one-bit matrix completion covers a broad range of real-life situations. In this paper, we propose a novel framework for one-bit matrix completion under the differential privacy constraint. In this framework, we develop several perturbation mechanisms and analyze the privacy-accuracy trade-off offered by each mechanism. The experiments conducted on both synthetic and real-world datasets demonstrate that our proposed approaches can maintain high-level privacy with little loss of completion accuracy.
Dense Color Constancy with Effective Edge Augmentation
Nov 17, 2019
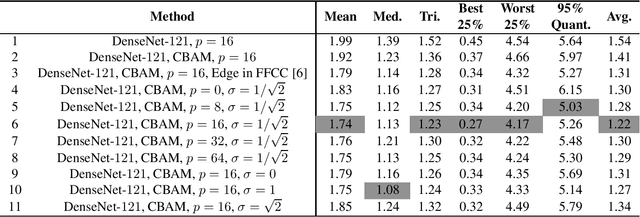
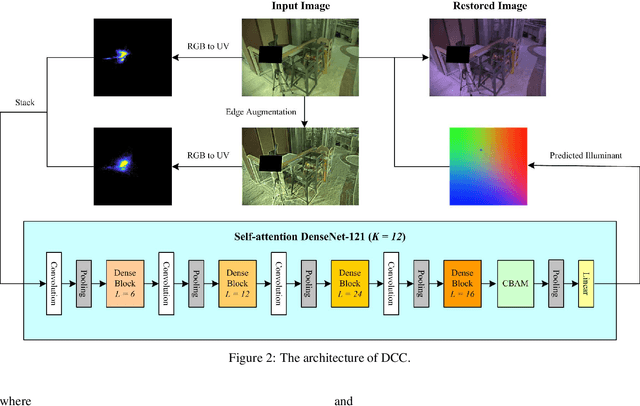
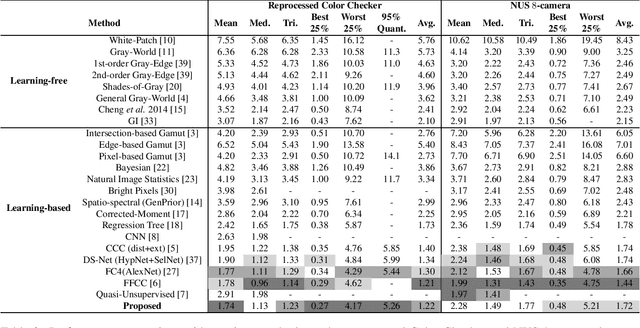
Abstract:Recently, computational color constancy via convolutional neural networks (CNNs) has received much attention. In this paper, we propose a color constancy algorithm called the Dense Color Constancy (DCC), which employs a self-attention DenseNet to estimate the illuminant based on the $2$D $\log$-chrominance histograms of input images and their augmented edges. The augmented edges help to tell apart the edge and non-edge pixels in the $\log$-histogram, which largely contribute to the feature extraction and color ambiguity elimination, thereby improving the accuracy of illuminant estimation. Experiments on benchmark datasets show that the DCC algorithm is very effective for illuminant estimation compared to the state-of-the-art methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge