LasTGL: An Industrial Framework for Large-Scale Temporal Graph Learning

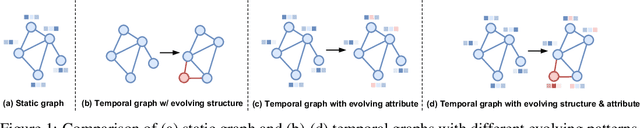
Over the past few years, graph neural networks (GNNs) have become powerful and practical tools for learning on (static) graph-structure data. However, many real-world applications, such as social networks and e-commerce, involve temporal graphs where nodes and edges are dynamically evolving. Temporal graph neural networks (TGNNs) have progressively emerged as an extension of GNNs to address time-evolving graphs and have gradually become a trending research topic in both academics and industry. Advancing research and application in such an emerging field necessitates the development of new tools to compose TGNN models and unify their different schemes for dealing with temporal graphs. In this work, we introduce LasTGL, an industrial framework that integrates unified and extensible implementations of common temporal graph learning algorithms for various advanced tasks. The purpose of LasTGL is to provide the essential building blocks for solving temporal graph learning tasks, focusing on the guiding principles of user-friendliness and quick prototyping on which PyTorch is based. In particular, LasTGL provides comprehensive temporal graph datasets, TGNN models and utilities along with well-documented tutorials, making it suitable for both absolute beginners and expert deep learning practitioners alike.

Hetero$^2$Net: Heterophily-aware Representation Learning on Heterogenerous Graphs

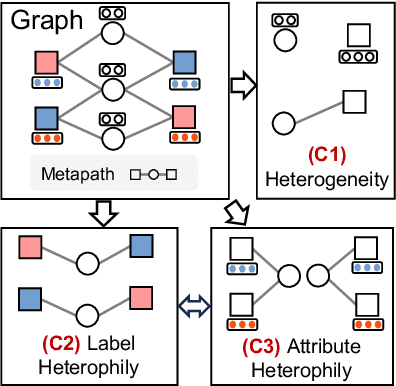
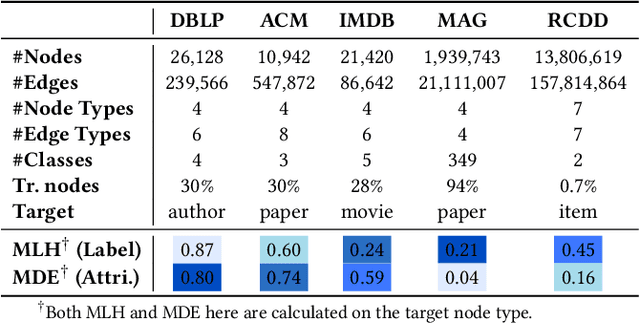
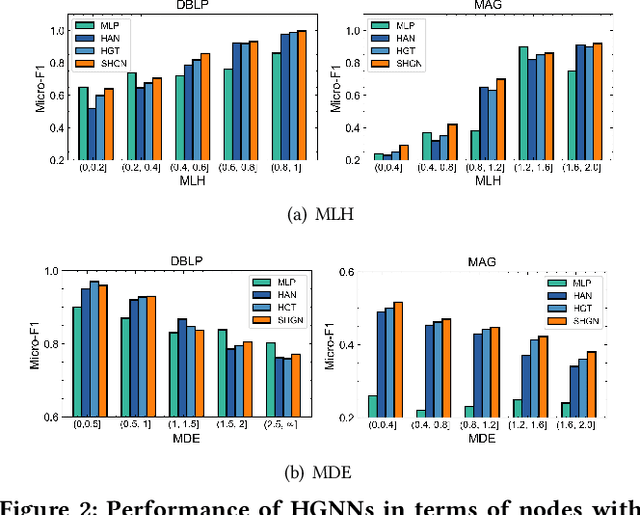
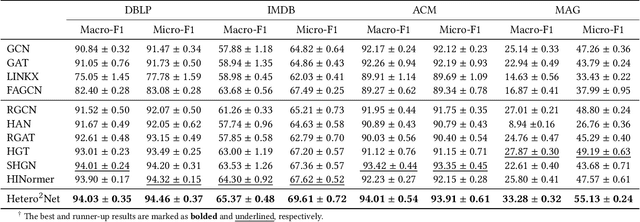
Real-world graphs are typically complex, exhibiting heterogeneity in the global structure, as well as strong heterophily within local neighborhoods. While a growing body of literature has revealed the limitations of common graph neural networks (GNNs) in handling homogeneous graphs with heterophily, little work has been conducted on investigating the heterophily properties in the context of heterogeneous graphs. To bridge this research gap, we identify the heterophily in heterogeneous graphs using metapaths and propose two practical metrics to quantitatively describe the levels of heterophily. Through in-depth investigations on several real-world heterogeneous graphs exhibiting varying levels of heterophily, we have observed that heterogeneous graph neural networks (HGNNs), which inherit many mechanisms from GNNs designed for homogeneous graphs, fail to generalize to heterogeneous graphs with heterophily or low level of homophily. To address the challenge, we present Hetero$^2$Net, a heterophily-aware HGNN that incorporates both masked metapath prediction and masked label prediction tasks to effectively and flexibly handle both homophilic and heterophilic heterogeneous graphs. We evaluate the performance of Hetero$^2$Net on five real-world heterogeneous graph benchmarks with varying levels of heterophily. The results demonstrate that Hetero$^2$Net outperforms strong baselines in the semi-supervised node classification task, providing valuable insights into effectively handling more complex heterogeneous graphs.

Self-supervision meets kernel graph neural models: From architecture to augmentations

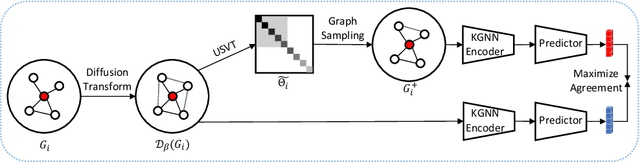
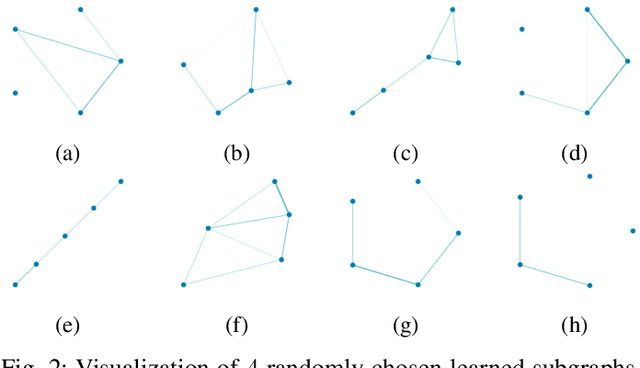
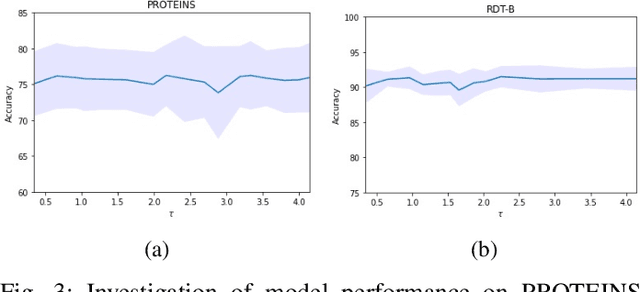
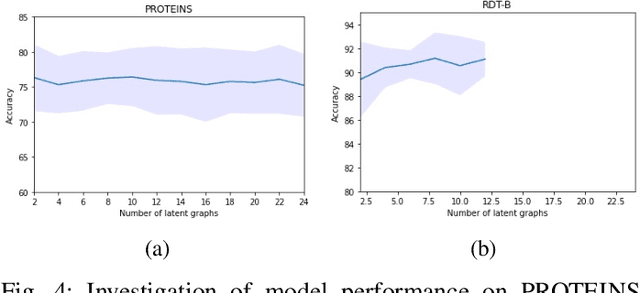
Graph representation learning has now become the de facto standard when handling graph-structured data, with the framework of message-passing graph neural networks (MPNN) being the most prevailing algorithmic tool. Despite its popularity, the family of MPNNs suffers from several drawbacks such as transparency and expressivity. Recently, the idea of designing neural models on graphs using the theory of graph kernels has emerged as a more transparent as well as sometimes more expressive alternative to MPNNs known as kernel graph neural networks (KGNNs). Developments on KGNNs are currently a nascent field of research, leaving several challenges from algorithmic design and adaptation to other learning paradigms such as self-supervised learning. In this paper, we improve the design and learning of KGNNs. Firstly, we extend the algorithmic formulation of KGNNs by allowing a more flexible graph-level similarity definition that encompasses former proposals like random walk graph kernel, as well as providing a smoother optimization objective that alleviates the need of introducing combinatorial learning procedures. Secondly, we enhance KGNNs through the lens of self-supervision via developing a novel structure-preserving graph data augmentation method called latent graph augmentation (LGA). Finally, we perform extensive empirical evaluations to demonstrate the efficacy of our proposed mechanisms. Experimental results over benchmark datasets suggest that our proposed model achieves competitive performance that is comparable to or sometimes outperforming state-of-the-art graph representation learning frameworks with or without self-supervision on graph classification tasks. Comparisons against other previously established graph data augmentation methods verify that the proposed LGA augmentation scheme captures better semantics of graph-level invariance.