Fast Graph Subset Selection Based on G-optimal Design

Graph sampling theory extends the traditional sampling theory to graphs with topological structures. As a key part of the graph sampling theory, subset selection chooses nodes on graphs as samples to reconstruct the original signal. Due to the eigen-decomposition operation for Laplacian matrices of graphs, however, existing subset selection methods usually require high-complexity calculations. In this paper, with an aim of enhancing the computational efficiency of subset selection on graphs, we propose a novel objective function based on the optimal experimental design. Theoretical analysis shows that this function enjoys an $\alpha$-supermodular property with a provable lower bound on $\alpha$. The objective function, together with an approximate of the low-pass filter on graphs, suggests a fast subset selection method that does not require any eigen-decomposition operation. Experimental results show that the proposed method exhibits high computational efficiency, while having competitive results compared to the state-of-the-art ones, especially when the sampling rate is low.

Applying Differential Privacy to Tensor Completion

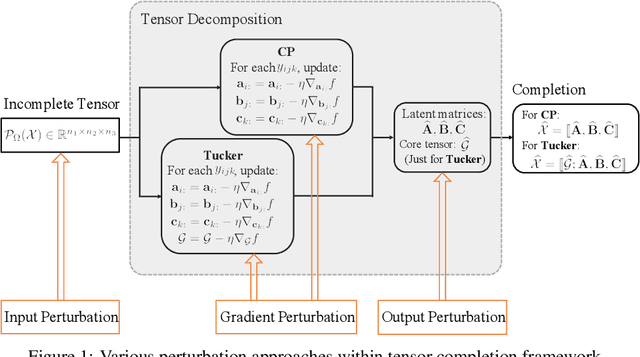
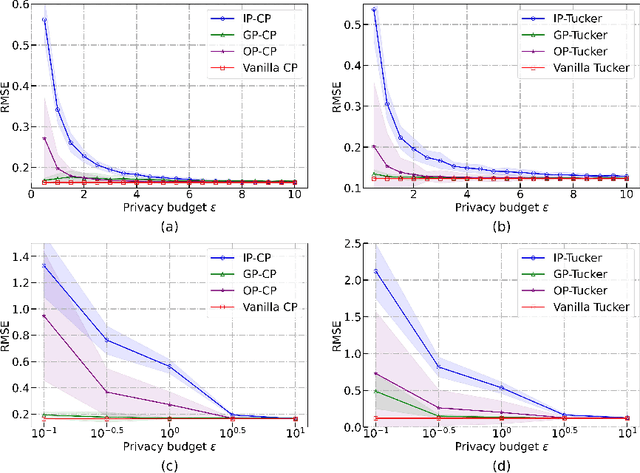
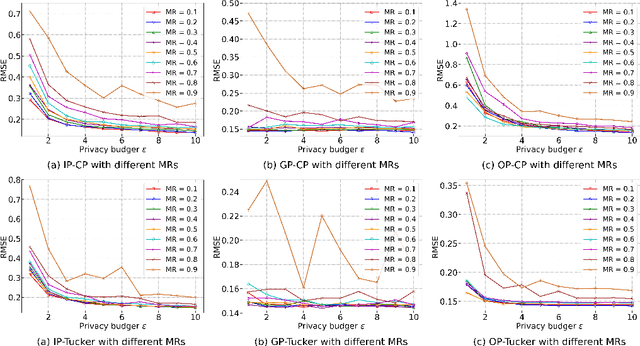
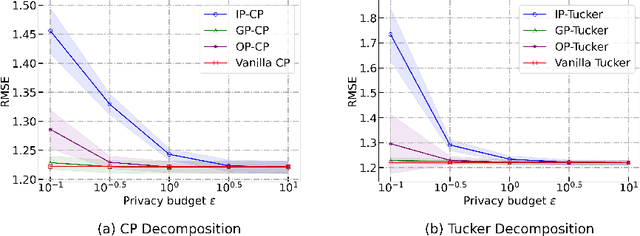
Tensor completion aims at filling the missing or unobserved entries based on partially observed tensors. However, utilization of the observed tensors often raises serious privacy concerns in many practical scenarios. To address this issue, we propose a solid and unified framework that contains several approaches for applying differential privacy to the two most widely used tensor decomposition methods: i) CANDECOMP/PARAFAC~(CP) and ii) Tucker decompositions. For each approach, we establish a rigorous privacy guarantee and meanwhile evaluate the privacy-accuracy trade-off. Experiments on synthetic and real-world datasets demonstrate that our proposal achieves high accuracy for tensor completion while ensuring strong privacy protections.

SAM: A Self-adaptive Attention Module for Context-Aware Recommendation System

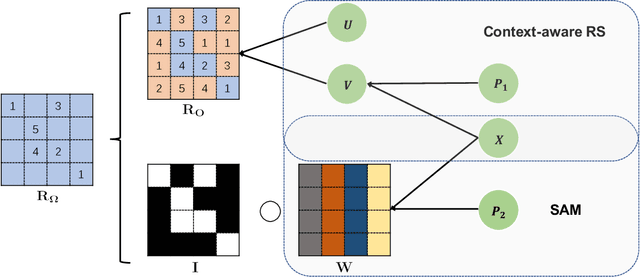
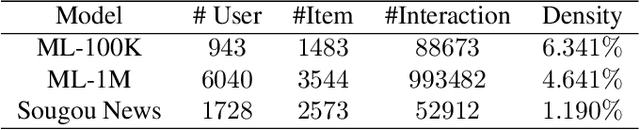
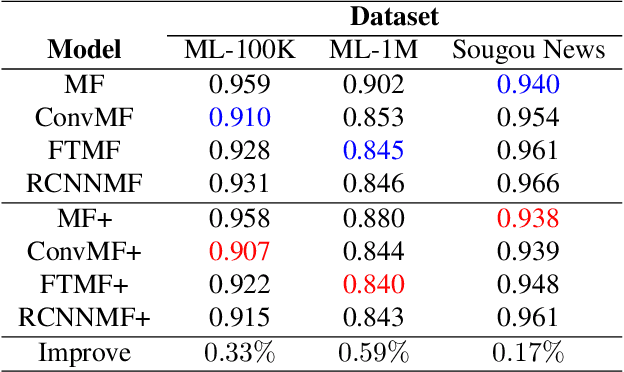
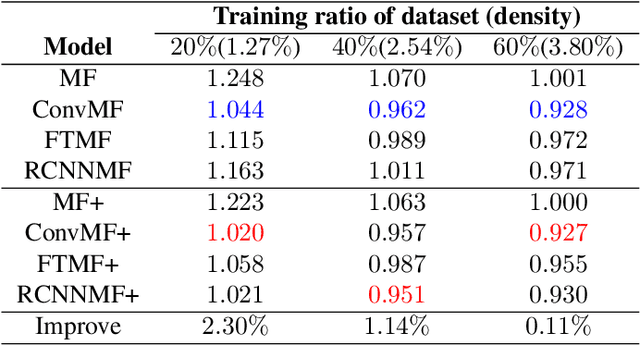
Recently, textual information has been proved to play a positive role in recommendation systems. However, most of the existing methods only focus on representation learning of textual information in ratings, while potential selection bias induced by the textual information is ignored. In this work, we propose a novel and general self-adaptive module, the Self-adaptive Attention Module (SAM), which adjusts the selection bias by capturing contextual information based on its representation. This module can be embedded into recommendation systems that contain learning components of contextual information. Experimental results on three real-world datasets demonstrate the effectiveness of our proposal, and the state-of-the-art models with SAM significantly outperform the original ones.

One-Bit Matrix Completion with Differential Privacy

Matrix completion is a prevailing collaborative filtering method for recommendation systems that requires the data offered by users to provide personalized service. However, due to insidious attacks and unexpected inference, the release of user data often raises serious privacy concerns. Most of the existing solutions focus on improving the privacy guarantee for general matrix completion. As a special case, in recommendation systems where the observations are binary, one-bit matrix completion covers a broad range of real-life situations. In this paper, we propose a novel framework for one-bit matrix completion under the differential privacy constraint. In this framework, we develop several perturbation mechanisms and analyze the privacy-accuracy trade-off offered by each mechanism. The experiments conducted on both synthetic and real-world datasets demonstrate that our proposed approaches can maintain high-level privacy with little loss of completion accuracy.