Efficient Two-Stage Gaussian Process Regression Via Automatic Kernel Search and Subsampling

Gaussian Process Regression (GPR) is widely used in statistics and machine learning for prediction tasks requiring uncertainty measures. Its efficacy depends on the appropriate specification of the mean function, covariance kernel function, and associated hyperparameters. Severe misspecifications can lead to inaccurate results and problematic consequences, especially in safety-critical applications. However, a systematic approach to handle these misspecifications is lacking in the literature. In this work, we propose a general framework to address these issues. Firstly, we introduce a flexible two-stage GPR framework that separates mean prediction and uncertainty quantification (UQ) to prevent mean misspecification, which can introduce bias into the model. Secondly, kernel function misspecification is addressed through a novel automatic kernel search algorithm, supported by theoretical analysis, that selects the optimal kernel from a candidate set. Additionally, we propose a subsampling-based warm-start strategy for hyperparameter initialization to improve efficiency and avoid hyperparameter misspecification. With much lower computational cost, our subsampling-based strategy can yield competitive or better performance than training exclusively on the full dataset. Combining all these components, we recommend two GPR methods-exact and scalable-designed to match available computational resources and specific UQ requirements. Extensive evaluation on real-world datasets, including UCI benchmarks and a safety-critical medical case study, demonstrates the robustness and precision of our methods.

MedDiff: Generating Electronic Health Records using Accelerated Denoising Diffusion Model

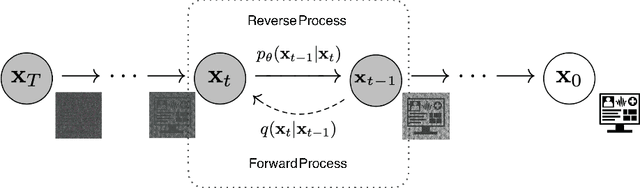
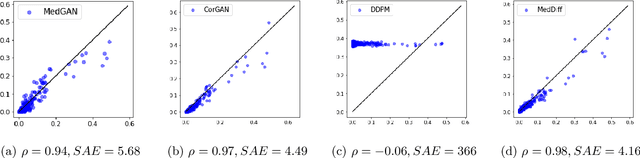
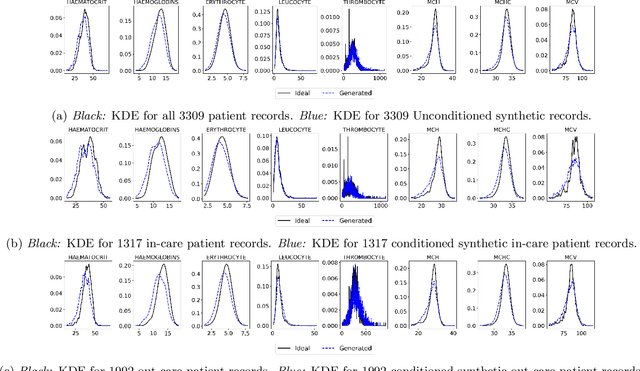
Due to patient privacy protection concerns, machine learning research in healthcare has been undeniably slower and limited than in other application domains. High-quality, realistic, synthetic electronic health records (EHRs) can be leveraged to accelerate methodological developments for research purposes while mitigating privacy concerns associated with data sharing. The current state-of-the-art model for synthetic EHR generation is generative adversarial networks, which are notoriously difficult to train and can suffer from mode collapse. Denoising Diffusion Probabilistic Models, a class of generative models inspired by statistical thermodynamics, have recently been shown to generate high-quality synthetic samples in certain domains. It is unknown whether these can generalize to generation of large-scale, high-dimensional EHRs. In this paper, we present a novel generative model based on diffusion models that is the first successful application on electronic health records. Our model proposes a mechanism to perform class-conditional sampling to preserve label information. We also introduce a new sampling strategy to accelerate the inference speed. We empirically show that our model outperforms existing state-of-the-art synthetic EHR generation methods.

MuG: A Multimodal Classification Benchmark on Game Data with Tabular, Textual, and Visual Fields

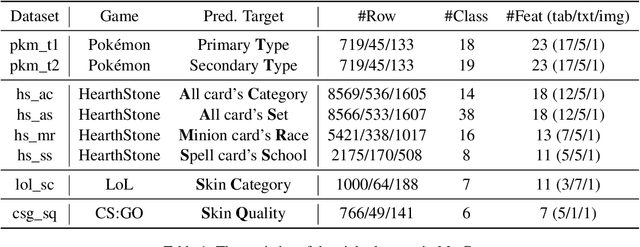
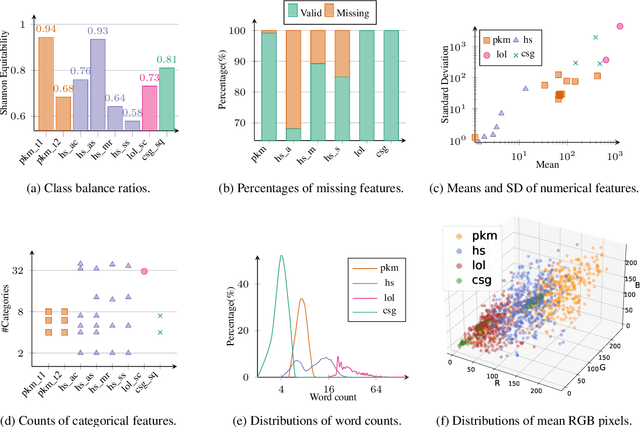
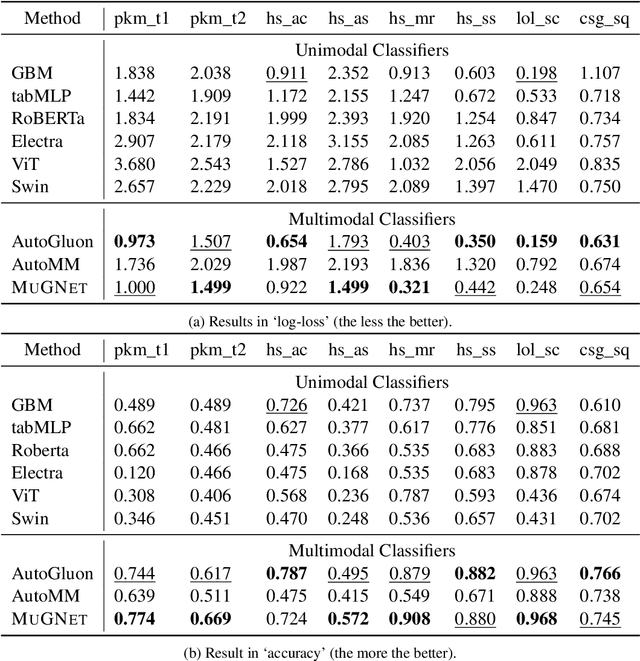
Multimodal learning has attracted the interest of the machine learning community due to its great potential in a variety of applications. To help achieve this potential, we propose a multimodal benchmark MuG with eight datasets allowing researchers to test the multimodal perceptron capabilities of their models. These datasets are collected from four different genres of games that cover tabular, textual, and visual modalities. We conduct multi-aspect data analysis to provide insights into the benchmark, including label balance ratios, percentages of missing features, distributions of data within each modality, and the correlations between labels and input modalities. We further present experimental results obtained by several state-of-the-art unimodal classifiers and multimodal classifiers, which demonstrate the challenging and multimodal-dependent properties of the benchmark. MuG is released at https://github.com/lujiaying/MUG-Bench with the data, documents, tutorials, and implemented baselines. Extensions of MuG are welcomed to facilitate the progress of research in multimodal learning problems.

An Efficient Nonlinear Acceleration method that Exploits Symmetry of the Hessian

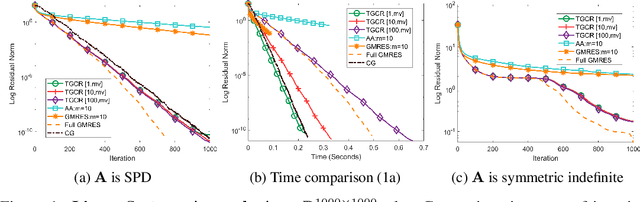
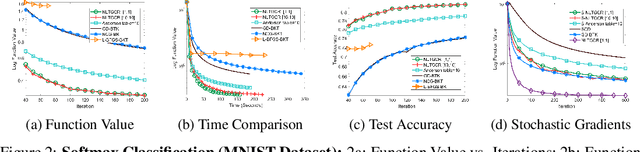
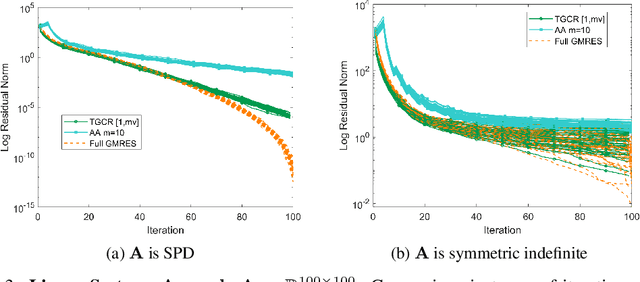
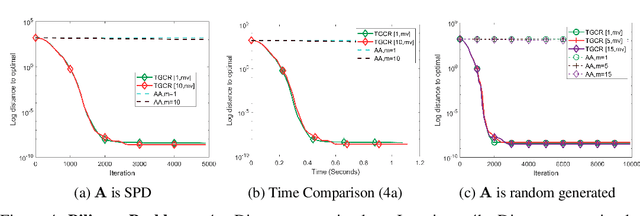
Nonlinear acceleration methods are powerful techniques to speed up fixed-point iterations. However, many acceleration methods require storing a large number of previous iterates and this can become impractical if computational resources are limited. In this paper, we propose a nonlinear Truncated Generalized Conjugate Residual method (nlTGCR) whose goal is to exploit the symmetry of the Hessian to reduce memory usage. The proposed method can be interpreted as either an inexact Newton or a quasi-Newton method. We show that, with the help of global strategies like residual check techniques, nlTGCR can converge globally for general nonlinear problems and that under mild conditions, nlTGCR is able to achieve superlinear convergence. We further analyze the convergence of nlTGCR in a stochastic setting. Numerical results demonstrate the superiority of nlTGCR when compared with several other competitive baseline approaches on a few problems. Our code will be available in the future.

Solve Minimax Optimization by Anderson Acceleration

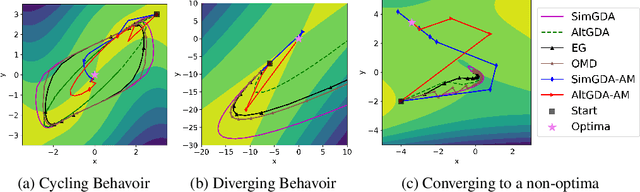
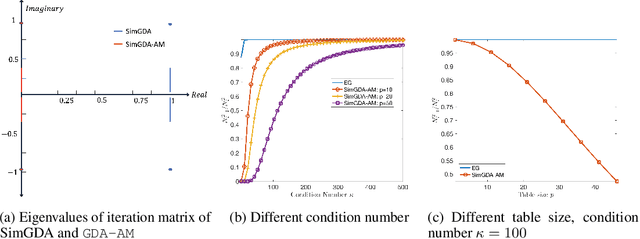
Many modern machine learning algorithms such as generative adversarial networks (GANs) and adversarial training can be formulated as minimax optimization. Gradient descent ascent (GDA) is the most commonly used algorithm due to its simplicity. However, GDA can converge to non-optimal minimax points. We propose a new minimax optimization framework, GDA-AM, that views the GDAdynamics as a fixed-point iteration and solves it using Anderson Mixing to con-verge to the local minimax. It addresses the diverging issue of simultaneous GDAand accelerates the convergence of alternating GDA. We show theoretically that the algorithm can achieve global convergence for bilinear problems under mild conditions. We also empirically show that GDA-AMsolves a variety of minimax problems and improves GAN training on several datasets