Sampling and multilevel coarsening algorithms for fast matrix approximations
Paper and Code
Oct 01, 2018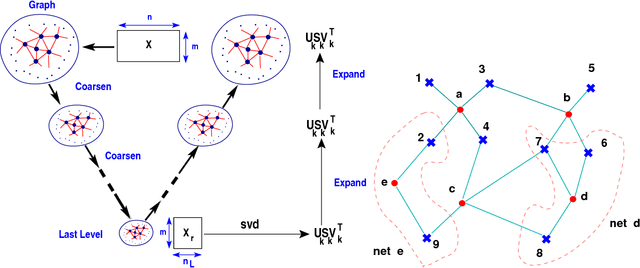
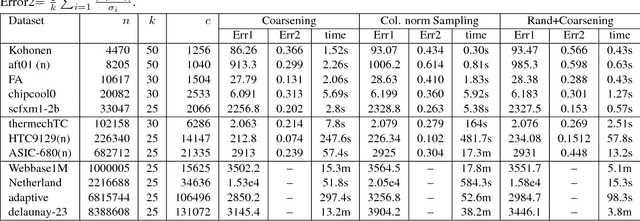
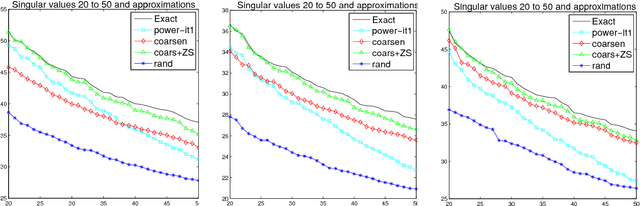
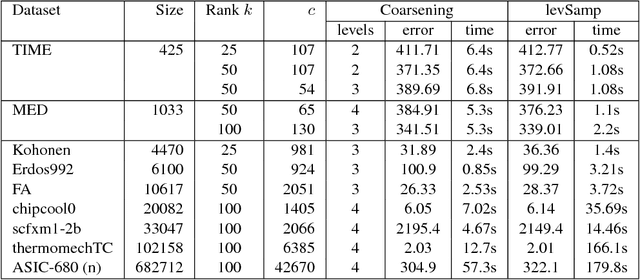
This paper addresses matrix approximation problems for matrices that are large, sparse and/or that are representations of large graphs. To tackle these problems, we consider algorithms that are based primarily on coarsening techniques, possibly combined with random sampling. A multilevel coarsening technique is proposed which utilizes a hypergraph associated with the data matrix and a graph coarsening strategy based on column matching. Theoretical results are established that characterize the quality of the dimension reduction achieved by a coarsening step, when a proper column matching strategy is employed. We consider a number of standard applications of this technique as well as a few new ones. Among the standard applications we first consider the problem of computing the partial SVD for which a combination of sampling and coarsening yields significantly improved SVD results relative to sampling alone. We also consider the Column subset selection problem, a popular low rank approximation method used in data related applications, and show how multilevel coarsening can be adapted for this problem. Similarly, we consider the problem of graph sparsification and show how coarsening techniques can be employed to solve it. Numerical experiments illustrate the performances of the methods in various applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge