Joint Registration and Conformal Prediction for Partially Observed Functional Data

Predicting missing segments in partially observed functions is challenging due to infinite-dimensionality, complex dependence within and across observations, and irregular noise. These challenges are further exacerbated by the existence of two distinct sources of variation in functional data, termed amplitude (variation along the $y$-axis) and phase (variation along the $x$-axis). While registration can disentangle them from complete functional data, the process is more difficult for partial observations. Thus, existing methods for functional data prediction often ignore phase variation. Furthermore, they rely on strong parametric assumptions, and require either precise model specifications or computationally intensive techniques, such as bootstrapping, to construct prediction intervals. To tackle this problem, we propose a unified registration and prediction approach for partially observed functions under the conformal prediction framework, which separately focuses on the amplitude and phase components. By leveraging split conformal methods, our approach integrates registration and prediction while ensuring exchangeability through carefully constructed predictor-response pairs. Using a neighborhood smoothing algorithm, the framework produces pointwise prediction bands with finite-sample marginal coverage guarantees under weak assumptions. The method is easy to implement, computationally efficient, and suitable for parallelization. Numerical studies and real-world data examples clearly demonstrate the effectiveness and practical utility of the proposed approach.

Modifying Final Splits of Classification Tree for Fine-tuning Subpopulation Target in Policy Making

Policymakers often use Classification and Regression Trees (CART) to partition populations based on binary outcomes and target subpopulations whose probability of the binary event exceeds a threshold. However, classic CART and knowledge distillation method whose student model is a CART (referred to as KD-CART) do not minimize the misclassification risk associated with classifying the latent probabilities of these binary events. To reduce the misclassification risk, we propose two methods, Penalized Final Split (PFS) and Maximizing Distance Final Split (MDFS). PFS incorporates a tunable penalty into the standard CART splitting criterion function. MDFS maximizes a weighted sum of distances between node means and the threshold. It can point-identify the optimal split under the unique intersect latent probability assumption. In addition, we develop theoretical result for MDFS splitting rule estimation, which has zero asymptotic risk. Through extensive simulation studies, we demonstrate that these methods predominately outperform classic CART and KD-CART in terms of misclassification error. Furthermore, in our empirical evaluations, these methods provide deeper insights than the two baseline methods.

Agri-LLaVA: Knowledge-Infused Large Multimodal Assistant on Agricultural Pests and Diseases

In the general domain, large multimodal models (LMMs) have achieved significant advancements, yet challenges persist in applying them to specific fields, especially agriculture. As the backbone of the global economy, agriculture confronts numerous challenges, with pests and diseases being particularly concerning due to their complexity, variability, rapid spread, and high resistance. This paper specifically addresses these issues. We construct the first multimodal instruction-following dataset in the agricultural domain, covering over 221 types of pests and diseases with approximately 400,000 data entries. This dataset aims to explore and address the unique challenges in pest and disease control. Based on this dataset, we propose a knowledge-infused training method to develop Agri-LLaVA, an agricultural multimodal conversation system. To accelerate progress in this field and inspire more researchers to engage, we design a diverse and challenging evaluation benchmark for agricultural pests and diseases. Experimental results demonstrate that Agri-LLaVA excels in agricultural multimodal conversation and visual understanding, providing new insights and approaches to address agricultural pests and diseases. By open-sourcing our dataset and model, we aim to promote research and development in LMMs within the agricultural domain and make significant contributions to tackle the challenges of agricultural pests and diseases. All resources can be found at https://github.com/Kki2Eve/Agri-LLaVA.

Probabilistic size-and-shape functional mixed models

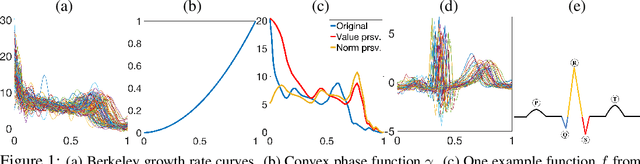
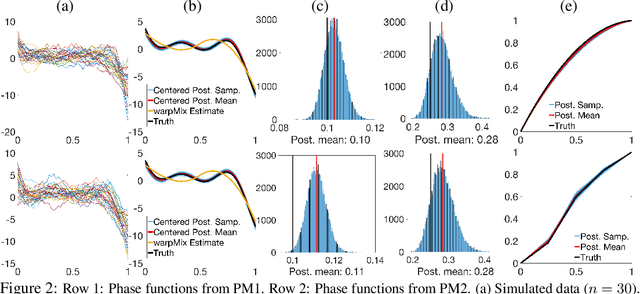
The reliable recovery and uncertainty quantification of a fixed effect function $\mu$ in a functional mixed model, for modelling population- and object-level variability in noisily observed functional data, is a notoriously challenging task: variations along the $x$ and $y$ axes are confounded with additive measurement error, and cannot in general be disentangled. The question then as to what properties of $\mu$ may be reliably recovered becomes important. We demonstrate that it is possible to recover the size-and-shape of a square-integrable $\mu$ under a Bayesian functional mixed model. The size-and-shape of $\mu$ is a geometric property invariant to a family of space-time unitary transformations, viewed as rotations of the Hilbert space, that jointly transform the $x$ and $y$ axes. A random object-level unitary transformation then captures size-and-shape \emph{preserving} deviations of $\mu$ from an individual function, while a random linear term and measurement error capture size-and-shape \emph{altering} deviations. The model is regularized by appropriate priors on the unitary transformations, posterior summaries of which may then be suitably interpreted as optimal data-driven rotations of a fixed orthonormal basis for the Hilbert space. Our numerical experiments demonstrate utility of the proposed model, and superiority over the current state-of-the-art.