Sebastian Kurtek
Joint Registration and Conformal Prediction for Partially Observed Functional Data
Feb 20, 2025Abstract:Predicting missing segments in partially observed functions is challenging due to infinite-dimensionality, complex dependence within and across observations, and irregular noise. These challenges are further exacerbated by the existence of two distinct sources of variation in functional data, termed amplitude (variation along the $y$-axis) and phase (variation along the $x$-axis). While registration can disentangle them from complete functional data, the process is more difficult for partial observations. Thus, existing methods for functional data prediction often ignore phase variation. Furthermore, they rely on strong parametric assumptions, and require either precise model specifications or computationally intensive techniques, such as bootstrapping, to construct prediction intervals. To tackle this problem, we propose a unified registration and prediction approach for partially observed functions under the conformal prediction framework, which separately focuses on the amplitude and phase components. By leveraging split conformal methods, our approach integrates registration and prediction while ensuring exchangeability through carefully constructed predictor-response pairs. Using a neighborhood smoothing algorithm, the framework produces pointwise prediction bands with finite-sample marginal coverage guarantees under weak assumptions. The method is easy to implement, computationally efficient, and suitable for parallelization. Numerical studies and real-world data examples clearly demonstrate the effectiveness and practical utility of the proposed approach.
Probabilistic size-and-shape functional mixed models
Nov 27, 2024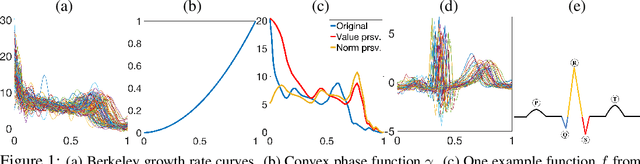

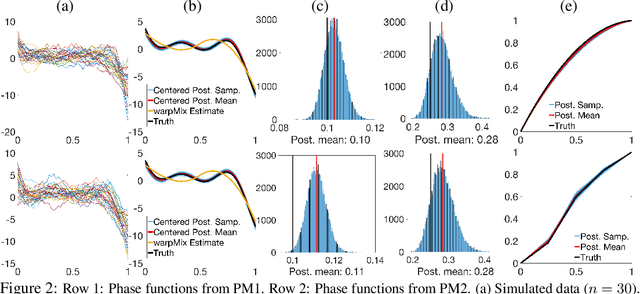

Abstract:The reliable recovery and uncertainty quantification of a fixed effect function $\mu$ in a functional mixed model, for modelling population- and object-level variability in noisily observed functional data, is a notoriously challenging task: variations along the $x$ and $y$ axes are confounded with additive measurement error, and cannot in general be disentangled. The question then as to what properties of $\mu$ may be reliably recovered becomes important. We demonstrate that it is possible to recover the size-and-shape of a square-integrable $\mu$ under a Bayesian functional mixed model. The size-and-shape of $\mu$ is a geometric property invariant to a family of space-time unitary transformations, viewed as rotations of the Hilbert space, that jointly transform the $x$ and $y$ axes. A random object-level unitary transformation then captures size-and-shape \emph{preserving} deviations of $\mu$ from an individual function, while a random linear term and measurement error capture size-and-shape \emph{altering} deviations. The model is regularized by appropriate priors on the unitary transformations, posterior summaries of which may then be suitably interpreted as optimal data-driven rotations of a fixed orthonormal basis for the Hilbert space. Our numerical experiments demonstrate utility of the proposed model, and superiority over the current state-of-the-art.
4D Atlas: Statistical Analysis of the Spatiotemporal Variability in Longitudinal 3D Shape Data
Jan 23, 2021
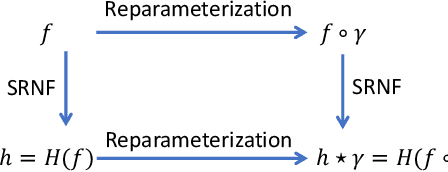


Abstract:We propose a novel framework to learn the spatiotemporal variability in longitudinal 3D shape data sets, which contain observations of subjects that evolve and deform over time. This problem is challenging since surfaces come with arbitrary spatial and temporal parameterizations. Thus, they need to be spatially registered and temporally aligned onto each other. We solve this spatiotemporal registration problem using a Riemannian approach. We treat a 3D surface as a point in a shape space equipped with an elastic metric that measures the amount of bending and stretching that the surfaces undergo. A 4D surface can then be seen as a trajectory in this space. With this formulation, the statistical analysis of 4D surfaces becomes the problem of analyzing trajectories embedded in a nonlinear Riemannian manifold. However, computing spatiotemporal registration and statistics on nonlinear spaces relies on complex nonlinear optimizations. Our core contribution is the mapping of the surfaces to the space of Square-Root Normal Fields (SRNF) where the L2 metric is equivalent to the partial elastic metric in the space of surfaces. By solving the spatial registration in the SRNF space, analyzing 4D surfaces becomes the problem of analyzing trajectories embedded in the SRNF space, which is Euclidean. Here, we develop the building blocks that enable such analysis. These include the spatiotemporal registration of arbitrarily parameterized 4D surfaces even in the presence of large elastic deformations and large variations in their execution rates, the computation of geodesics between 4D surfaces, the computation of statistical summaries, such as means and modes of variation, and the synthesis of random 4D surfaces. We demonstrate the performance of the proposed framework using 4D facial surfaces and 4D human body shapes.
KShapeNet: Riemannian network on Kendall shape space for Skeleton based Action Recognition
Nov 24, 2020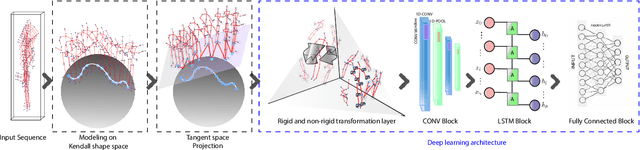
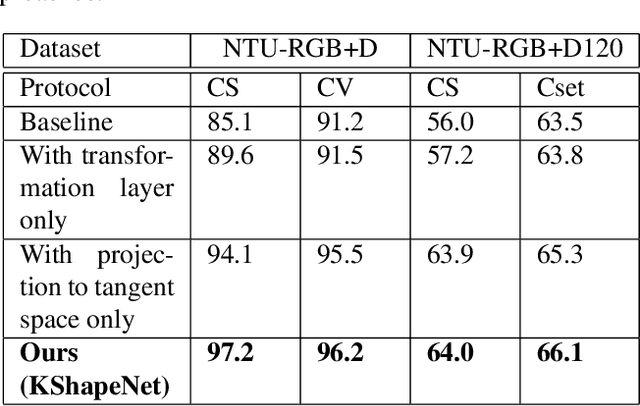
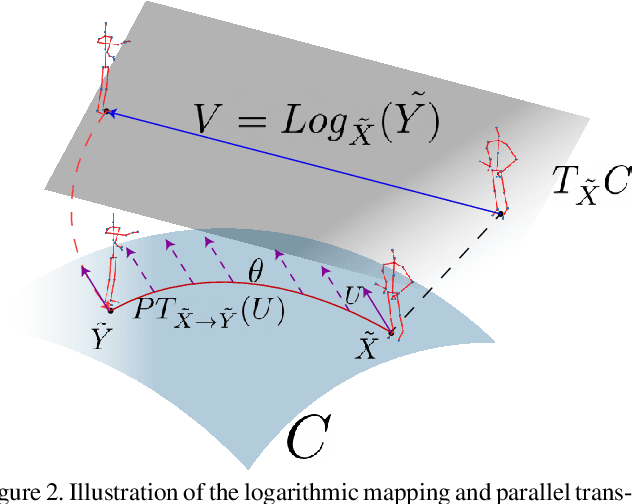
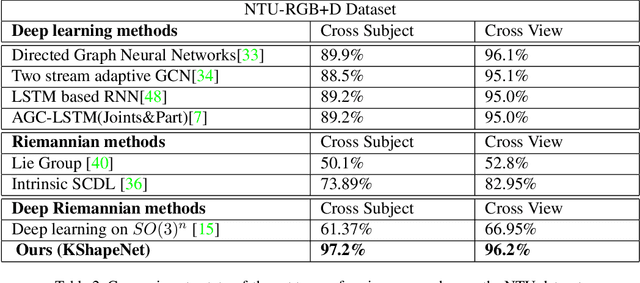
Abstract:Deep Learning architectures, albeit successful in most computer vision tasks, were designed for data with an underlying Euclidean structure, which is not usually fulfilled since pre-processed data may lie on a non-linear space. In this paper, we propose a geometry aware deep learning approach for skeleton-based action recognition. Skeleton sequences are first modeled as trajectories on Kendall's shape space and then mapped to the linear tangent space. The resulting structured data are then fed to a deep learning architecture, which includes a layer that optimizes over rigid and non rigid transformations of the 3D skeletons, followed by a CNN-LSTM network. The assessment on two large scale skeleton datasets, namely NTU-RGB+D and NTU-RGB+D 120, has proven that proposed approach outperforms existing geometric deep learning methods and is competitive with respect to recently published approaches.
Aggregated Pairwise Classification of Statistical Shapes
Jan 22, 2019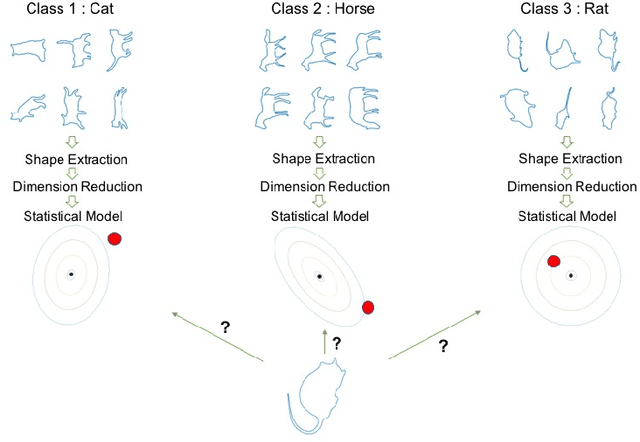
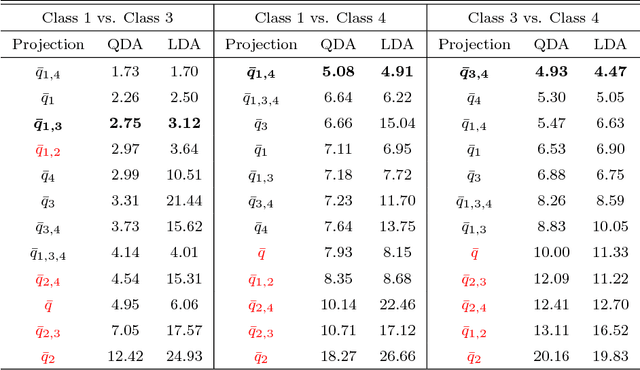

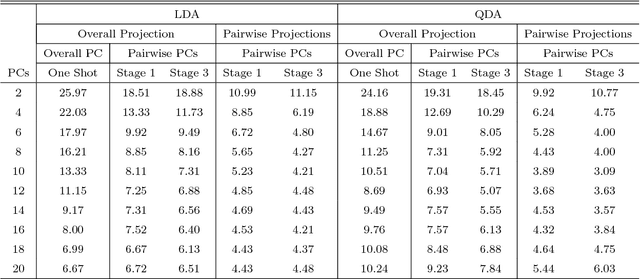
Abstract:The classification of shapes is of great interest in diverse areas ranging from medical imaging to computer vision and beyond. While many statistical frameworks have been developed for the classification problem, most are strongly tied to early formulations of the problem - with an object to be classified described as a vector in a relatively low-dimensional Euclidean space. Statistical shape data have two main properties that suggest a need for a novel approach: (i) shapes are inherently infinite dimensional with strong dependence among the positions of nearby points, and (ii) shape space is not Euclidean, but is fundamentally curved. To accommodate these features of the data, we work with the square-root velocity function of the curves to provide a useful formal description of the shape, pass to tangent spaces of the manifold of shapes at different projection points which effectively separate shapes for pairwise classification in the training data, and use principal components within these tangent spaces to reduce dimensionality. We illustrate the impact of the projection point and choice of subspace on the misclassification rate with a novel method of combining pairwise classifiers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge