Steven N. MacEachern
Aggregated Pairwise Classification of Statistical Shapes
Jan 22, 2019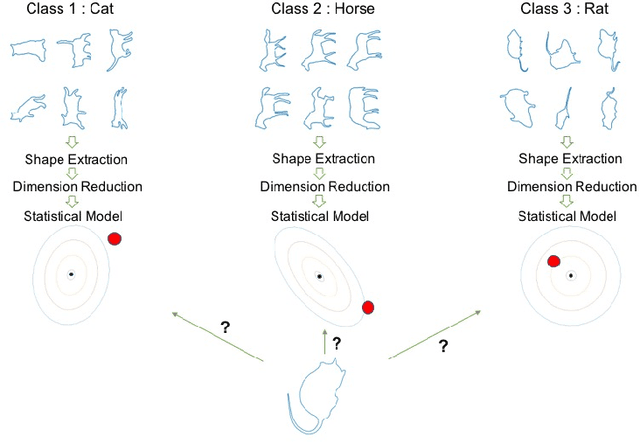
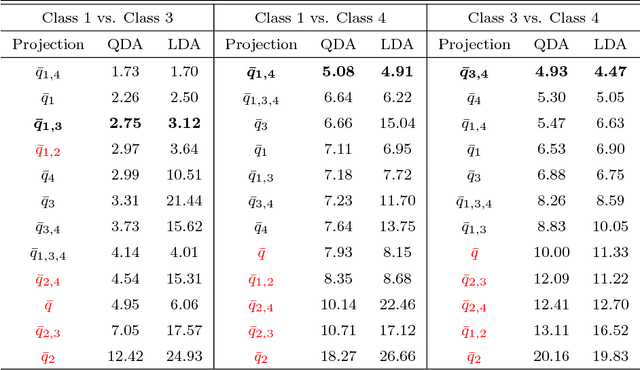

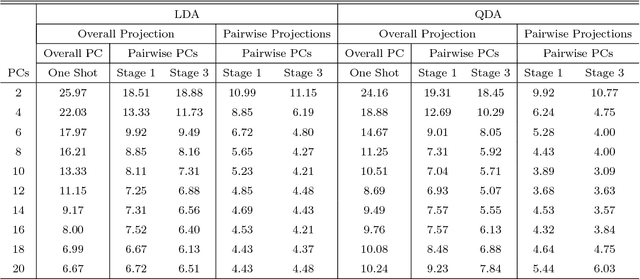
Abstract:The classification of shapes is of great interest in diverse areas ranging from medical imaging to computer vision and beyond. While many statistical frameworks have been developed for the classification problem, most are strongly tied to early formulations of the problem - with an object to be classified described as a vector in a relatively low-dimensional Euclidean space. Statistical shape data have two main properties that suggest a need for a novel approach: (i) shapes are inherently infinite dimensional with strong dependence among the positions of nearby points, and (ii) shape space is not Euclidean, but is fundamentally curved. To accommodate these features of the data, we work with the square-root velocity function of the curves to provide a useful formal description of the shape, pass to tangent spaces of the manifold of shapes at different projection points which effectively separate shapes for pairwise classification in the training data, and use principal components within these tangent spaces to reduce dimensionality. We illustrate the impact of the projection point and choice of subspace on the misclassification rate with a novel method of combining pairwise classifiers.
Restricting exchangeable nonparametric distributions
Sep 05, 2012



Abstract:Distributions over exchangeable matrices with infinitely many columns, such as the Indian buffet process, are useful in constructing nonparametric latent variable models. However, the distribution implied by such models over the number of features exhibited by each data point may be poorly- suited for many modeling tasks. In this paper, we propose a class of exchangeable nonparametric priors obtained by restricting the domain of existing models. Such models allow us to specify the distribution over the number of features per data point, and can achieve better performance on data sets where the number of features is not well-modeled by the original distribution.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge