4D Atlas: Statistical Analysis of the Spatiotemporal Variability in Longitudinal 3D Shape Data

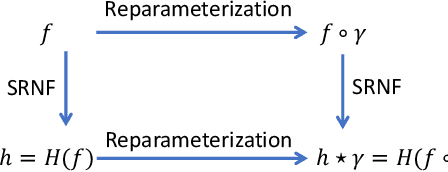
We propose a novel framework to learn the spatiotemporal variability in longitudinal 3D shape data sets, which contain observations of subjects that evolve and deform over time. This problem is challenging since surfaces come with arbitrary spatial and temporal parameterizations. Thus, they need to be spatially registered and temporally aligned onto each other. We solve this spatiotemporal registration problem using a Riemannian approach. We treat a 3D surface as a point in a shape space equipped with an elastic metric that measures the amount of bending and stretching that the surfaces undergo. A 4D surface can then be seen as a trajectory in this space. With this formulation, the statistical analysis of 4D surfaces becomes the problem of analyzing trajectories embedded in a nonlinear Riemannian manifold. However, computing spatiotemporal registration and statistics on nonlinear spaces relies on complex nonlinear optimizations. Our core contribution is the mapping of the surfaces to the space of Square-Root Normal Fields (SRNF) where the L2 metric is equivalent to the partial elastic metric in the space of surfaces. By solving the spatial registration in the SRNF space, analyzing 4D surfaces becomes the problem of analyzing trajectories embedded in the SRNF space, which is Euclidean. Here, we develop the building blocks that enable such analysis. These include the spatiotemporal registration of arbitrarily parameterized 4D surfaces even in the presence of large elastic deformations and large variations in their execution rates, the computation of geodesics between 4D surfaces, the computation of statistical summaries, such as means and modes of variation, and the synthesis of random 4D surfaces. We demonstrate the performance of the proposed framework using 4D facial surfaces and 4D human body shapes.

Bayesian shape modelling of cross-sectional geological data

Shape information is of great importance in many applications. For example, the oil-bearing capacity of sand bodies, the subterranean remnants of ancient rivers, is related to their cross-sectional shapes. The analysis of these shapes is therefore of some interest, but current classifications are simplistic and ad hoc. In this paper, we describe the first steps towards a coherent statistical analysis of these shapes by deriving the integrated likelihood for data shapes given class parameters. The result is of interest beyond this particular application.

Numerical Inversion of SRNF Maps for Elastic Shape Analysis of Genus-Zero Surfaces

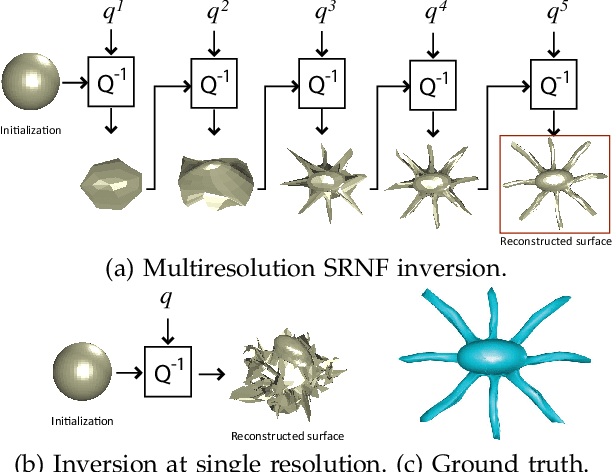
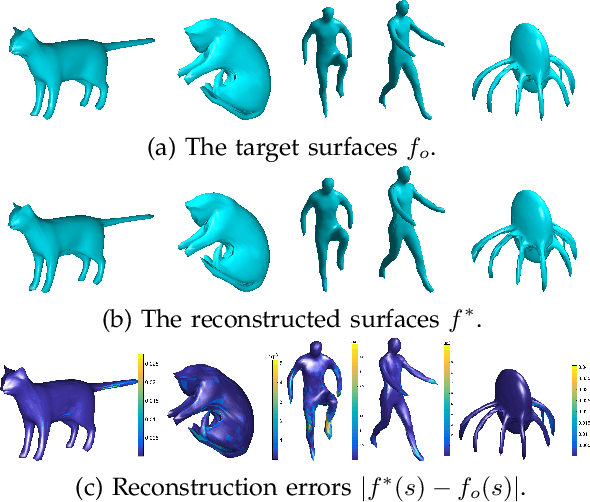
Recent developments in elastic shape analysis (ESA) are motivated by the fact that it provides comprehensive frameworks for simultaneous registration, deformation, and comparison of shapes. These methods achieve computational efficiency using certain square-root representations that transform invariant elastic metrics into Euclidean metrics, allowing for applications of standard algorithms and statistical tools. For analyzing shapes of embeddings of $\mathbb{S}^2$ in $\mathbb{R}^3$, Jermyn et al. introduced square-root normal fields (SRNFs) that transformed an elastic metric, with desirable invariant properties, into the $\mathbb{L}^2$ metric. These SRNFs are essentially surface normals scaled by square-roots of infinitesimal area elements. A critical need in shape analysis is to invert solutions (deformations, averages, modes of variations, etc) computed in the SRNF space, back to the original surface space for visualizations and inferences. Due to the lack of theory for understanding SRNFs maps and their inverses, we take a numerical approach and derive an efficient multiresolution algorithm, based on solving an optimization problem in the surface space, that estimates surfaces corresponding to given SRNFs. This solution is found effective, even for complex shapes, e.g. human bodies and animals, that undergo significant deformations including bending and stretching. Specifically, we use this inversion for computing elastic shape deformations, transferring deformations, summarizing shapes, and for finding modes of variability in a given collection, while simultaneously registering the surfaces. We demonstrate the proposed algorithms using a statistical analysis of human body shapes, classification of generic surfaces and analysis of brain structures.