4D Atlas: Statistical Analysis of the Spatiotemporal Variability in Longitudinal 3D Shape Data

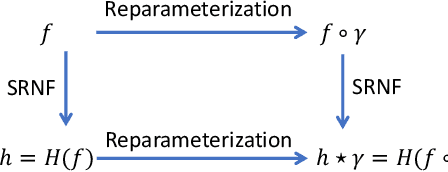
We propose a novel framework to learn the spatiotemporal variability in longitudinal 3D shape data sets, which contain observations of subjects that evolve and deform over time. This problem is challenging since surfaces come with arbitrary spatial and temporal parameterizations. Thus, they need to be spatially registered and temporally aligned onto each other. We solve this spatiotemporal registration problem using a Riemannian approach. We treat a 3D surface as a point in a shape space equipped with an elastic metric that measures the amount of bending and stretching that the surfaces undergo. A 4D surface can then be seen as a trajectory in this space. With this formulation, the statistical analysis of 4D surfaces becomes the problem of analyzing trajectories embedded in a nonlinear Riemannian manifold. However, computing spatiotemporal registration and statistics on nonlinear spaces relies on complex nonlinear optimizations. Our core contribution is the mapping of the surfaces to the space of Square-Root Normal Fields (SRNF) where the L2 metric is equivalent to the partial elastic metric in the space of surfaces. By solving the spatial registration in the SRNF space, analyzing 4D surfaces becomes the problem of analyzing trajectories embedded in the SRNF space, which is Euclidean. Here, we develop the building blocks that enable such analysis. These include the spatiotemporal registration of arbitrarily parameterized 4D surfaces even in the presence of large elastic deformations and large variations in their execution rates, the computation of geodesics between 4D surfaces, the computation of statistical summaries, such as means and modes of variation, and the synthesis of random 4D surfaces. We demonstrate the performance of the proposed framework using 4D facial surfaces and 4D human body shapes.