Numerical Inversion of SRNF Maps for Elastic Shape Analysis of Genus-Zero Surfaces
Paper and Code
Oct 14, 2016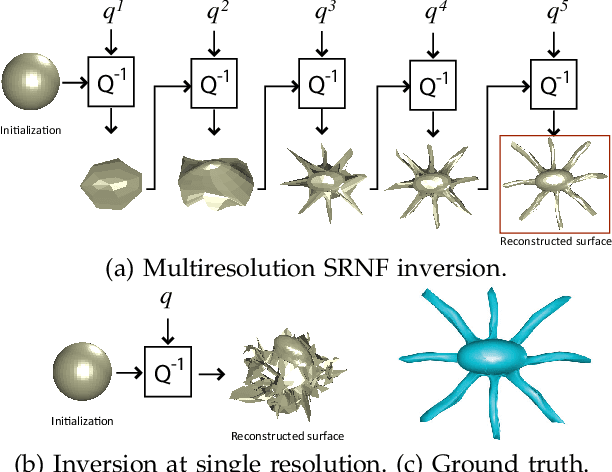

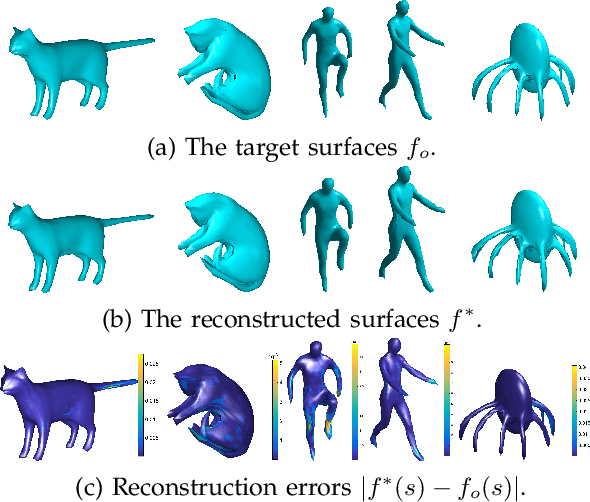

Recent developments in elastic shape analysis (ESA) are motivated by the fact that it provides comprehensive frameworks for simultaneous registration, deformation, and comparison of shapes. These methods achieve computational efficiency using certain square-root representations that transform invariant elastic metrics into Euclidean metrics, allowing for applications of standard algorithms and statistical tools. For analyzing shapes of embeddings of $\mathbb{S}^2$ in $\mathbb{R}^3$, Jermyn et al. introduced square-root normal fields (SRNFs) that transformed an elastic metric, with desirable invariant properties, into the $\mathbb{L}^2$ metric. These SRNFs are essentially surface normals scaled by square-roots of infinitesimal area elements. A critical need in shape analysis is to invert solutions (deformations, averages, modes of variations, etc) computed in the SRNF space, back to the original surface space for visualizations and inferences. Due to the lack of theory for understanding SRNFs maps and their inverses, we take a numerical approach and derive an efficient multiresolution algorithm, based on solving an optimization problem in the surface space, that estimates surfaces corresponding to given SRNFs. This solution is found effective, even for complex shapes, e.g. human bodies and animals, that undergo significant deformations including bending and stretching. Specifically, we use this inversion for computing elastic shape deformations, transferring deformations, summarizing shapes, and for finding modes of variability in a given collection, while simultaneously registering the surfaces. We demonstrate the proposed algorithms using a statistical analysis of human body shapes, classification of generic surfaces and analysis of brain structures.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge