Probabilistic size-and-shape functional mixed models
Paper and Code
Nov 27, 2024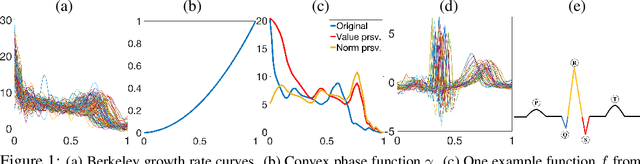

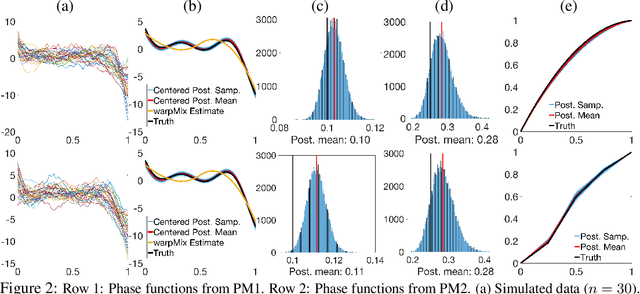

The reliable recovery and uncertainty quantification of a fixed effect function $\mu$ in a functional mixed model, for modelling population- and object-level variability in noisily observed functional data, is a notoriously challenging task: variations along the $x$ and $y$ axes are confounded with additive measurement error, and cannot in general be disentangled. The question then as to what properties of $\mu$ may be reliably recovered becomes important. We demonstrate that it is possible to recover the size-and-shape of a square-integrable $\mu$ under a Bayesian functional mixed model. The size-and-shape of $\mu$ is a geometric property invariant to a family of space-time unitary transformations, viewed as rotations of the Hilbert space, that jointly transform the $x$ and $y$ axes. A random object-level unitary transformation then captures size-and-shape \emph{preserving} deviations of $\mu$ from an individual function, while a random linear term and measurement error capture size-and-shape \emph{altering} deviations. The model is regularized by appropriate priors on the unitary transformations, posterior summaries of which may then be suitably interpreted as optimal data-driven rotations of a fixed orthonormal basis for the Hilbert space. Our numerical experiments demonstrate utility of the proposed model, and superiority over the current state-of-the-art.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge