Pete Trautman
Inverse Mixed Strategy Games with Generative Trajectory Models
Feb 05, 2025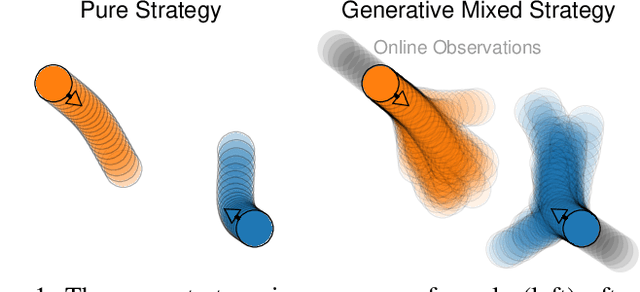
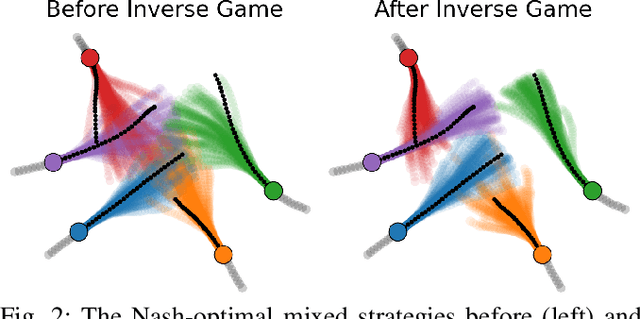
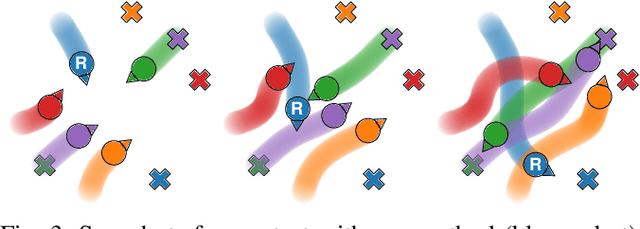
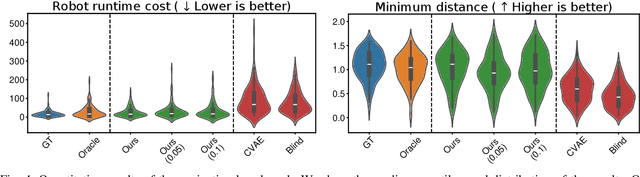
Abstract:Game-theoretic models are effective tools for modeling multi-agent interactions, especially when robots need to coordinate with humans. However, applying these models requires inferring their specifications from observed behaviors -- a challenging task known as the inverse game problem. Existing inverse game approaches often struggle to account for behavioral uncertainty and measurement noise, and leverage both offline and online data. To address these limitations, we propose an inverse game method that integrates a generative trajectory model into a differentiable mixed-strategy game framework. By representing the mixed strategy with a conditional variational autoencoder (CVAE), our method can infer high-dimensional, multi-modal behavior distributions from noisy measurements while adapting in real-time to new observations. We extensively evaluate our method in a simulated navigation benchmark, where the observations are generated by an unknown game model. Despite the model mismatch, our method can infer Nash-optimal actions comparable to those of the ground-truth model and the oracle inverse game baseline, even in the presence of uncertain agent objectives and noisy measurements.
Core Challenges of Social Robot Navigation: A Survey
Mar 17, 2021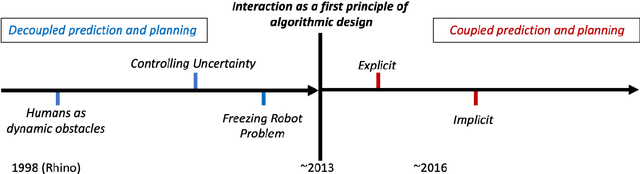



Abstract:Robot navigation in crowded public spaces is a complex task that requires addressing a variety of engineering and human factors challenges. These challenges have motivated a great amount of research resulting in important developments for the fields of robotics and human-robot interaction over the past three decades. Despite the significant progress and the massive recent interest, we observe a number of significant remaining challenges that prohibit the seamless deployment of autonomous robots in public pedestrian environments. In this survey article, we organize existing challenges into a set of categories related to broader open problems in motion planning, behavior design, and evaluation methodologies. Within these categories, we review past work, and offer directions for future research. Our work builds upon and extends earlier survey efforts by a) taking a critical perspective and diagnosing fundamental limitations of adopted practices in the field and b) offering constructive feedback and ideas that we aspire will drive research in the field over the coming decade.
Dynamic Channel: A Planning Framework for Crowd Navigation
Mar 01, 2019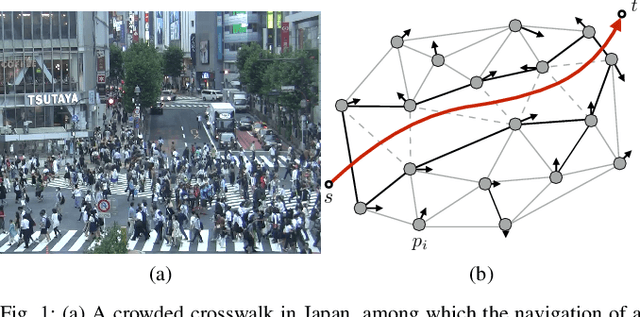
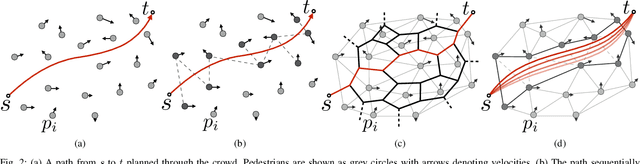
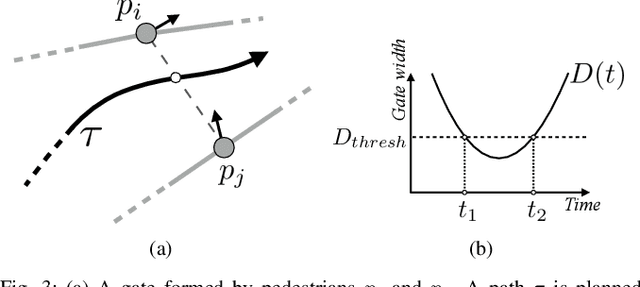
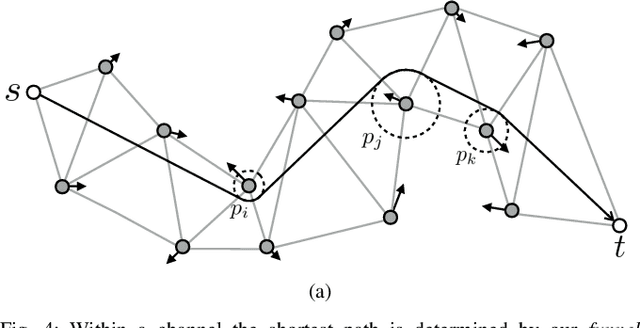
Abstract:Real-time navigation in dense human environments is a challenging problem in robotics. Most existing path planners fail to account for the dynamics of pedestrians because introducing time as an additional dimension in search space is computationally prohibitive. Alternatively, most local motion planners only address imminent collision avoidance and fail to offer long-term optimality. In this work, we present an approach, called Dynamic Channels, to solve this global to local quandary. Our method combines the high-level topological path planning with low-level motion planning into a complete pipeline. By formulating the path planning problem as graph searching in the triangulation space, our planner is able to explicitly reason about the obstacle dynamics and capture the environmental change efficiently. We evaluate efficiency and performance of our approach on public pedestrian datasets and compare it to a state-of-the-art planning algorithm for dynamic obstacle avoidance.
Generalized Shared Control versus Classical Shared Control: Illustrative Examples
May 28, 2017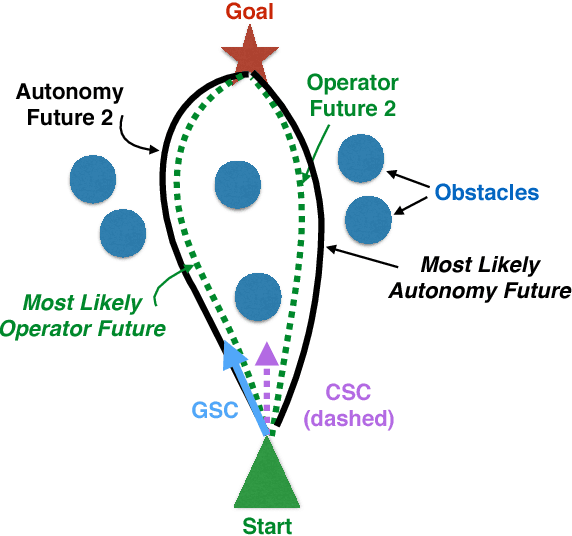
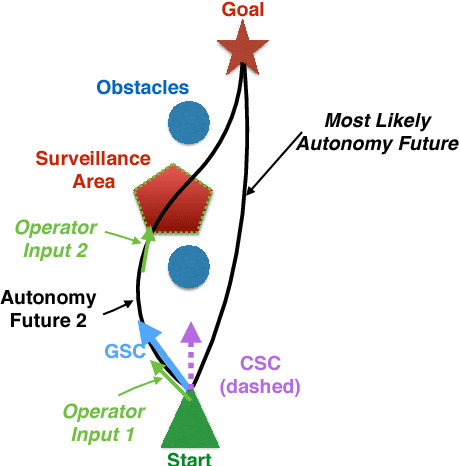

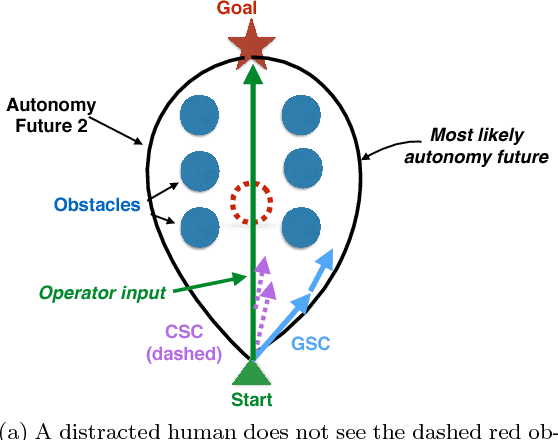
Abstract:Shared control fuses operator inputs and autonomy inputs into a single command. However, if environmental or operator predictions are multimodal, state of the art approaches are suboptimal with respect to safety, efficiency, and operator-autonomy agreement: even under mildly challenging conditions, existing approaches can fuse two safe inputs into an unsafe shared control [13]. Multi-modal conditions are common to many real world applications, such as search and rescue robots navigating disaster zones, teleoperated robots facing communication degradation, and assistive driving technologies. In [11, 13], we introduced a novel approach called generalized shared control (GSC) that simultaneously optimizes autonomy objectives (e.g., safety and efficiency) and operator-autonomy agreement under multimodal conditions; this optimality prevents such unsafe shared control. In this paper, we describe those results in more user friendly language by using illustrations and text.
Manifold Relevance Determination: Learning the Latent Space of Robotics
May 23, 2017
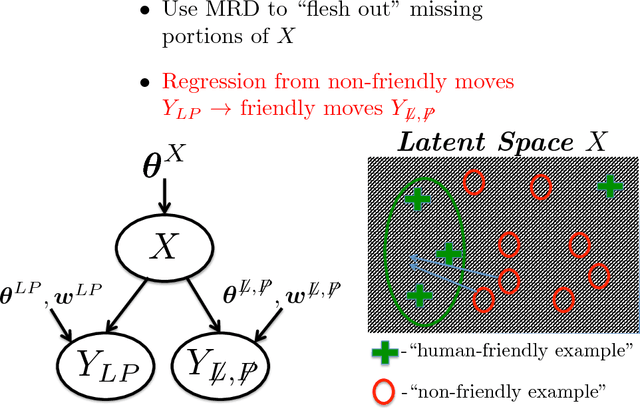
Abstract:In this article we present the basics of manifold relevance determination (MRD) as introduced in \cite{mrd}, and some applications where the technology might be of particular use. Section 1 acts as a short tutorial of the ideas developed in \cite{mrd}, while Section 2 presents possible applications in sensor fusion, multi-agent SLAM, and "human-appropriate" robot movement (e.g. legibility and predictability~\cite{dragan-hri-2013}). In particular, we show how MRD can be used to construct the underlying models in a data driven manner, rather than directly leveraging first principles theories (e.g., physics, psychology) as is commonly the case for sensor fusion, SLAM, and human robot interaction. We note that [Bekiroglu et al., 2016] leveraged MRD for correcting unstable robot grasps to stable robot grasps.
Sparse Interacting Gaussian Processes: Efficiency and Optimality Theorems of Autonomous Crowd Navigation
May 10, 2017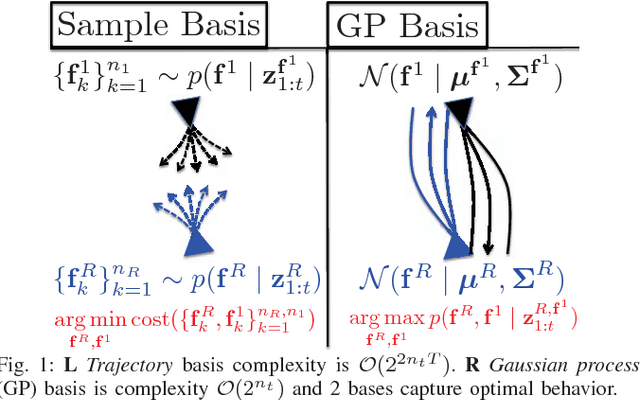

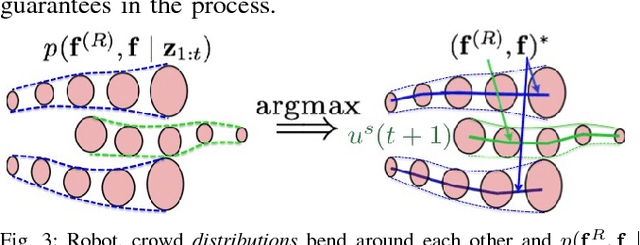
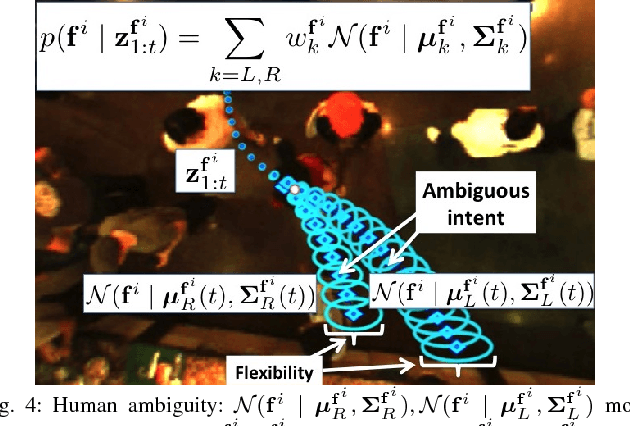
Abstract:We study the sparsity and optimality properties of crowd navigation and find that existing techniques do not satisfy both criteria simultaneously: either they achieve optimality with a prohibitive number of samples or tractability assumptions make them fragile to catastrophe. For example, if the human and robot are modeled independently, then tractability is attained but the planner is prone to overcautious or overaggressive behavior. For sampling based motion planning of joint human-robot cost functions, for $n_t$ agents and $T$ step lookahead, $\mathcal O(2^{2n_t T})$ samples are needed for coverage of the action space. Advanced approaches statically partition the action space into free-space and then sample in those convex regions. However, if the human is \emph{moving} into free-space, then the partition is misleading and sampling is unsafe: free space will soon be occupied. We diagnose the cause of these deficiencies---optimization happens over \emph{trajectory} space---and propose a novel solution: optimize over trajectory \emph{distribution} space by using a Gaussian process (GP) basis. We exploit the "kernel trick" of GPs, where a continuum of trajectories are captured with a mean and covariance function. By using the mean and covariance as proxies for a trajectory family we reason about collective trajectory behavior without resorting to sampling. The GP basis is sparse and optimal with respect to collision avoidance and robot and crowd intention and flexibility. GP sparsity leans heavily on the insight that joint action space decomposes into free regions; however, the decomposition contains feasible solutions only if the partition is dynamically generated. We call our approach \emph{$\mathcal O(2^{n_t})$-sparse interacting Gaussian processes}.
A Mathematical Theory of Human Machine Teaming
May 08, 2017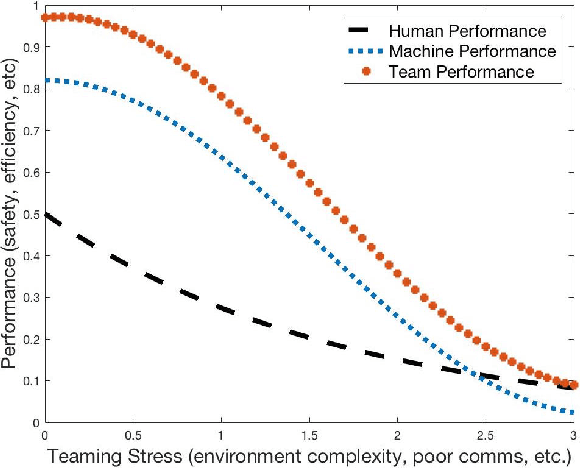


Abstract:We begin with a disquieting paradox: human machine teaming (HMT) often produces results worse than either the human or machine would produce alone. Critically, this failure is not a result of inferior human modeling or a suboptimal autonomy: even with perfect knowledge of human intention and perfect autonomy performance, prevailing teaming architectures still fail under trivial stressors~\cite{trautman-smc-2015}. This failure is instead a result of deficiencies at the \emph{decision fusion level}. Accordingly, \emph{efforts aimed solely at improving human prediction or improving autonomous performance will not produce acceptable HMTs: we can no longer model humans, machines and adversaries as distinct entities.} We thus argue for a strong but essential condition: HMTs should perform no worse than either member of the team alone, and this performance bound should be independent of environment complexity, human-machine interfacing, accuracy of the human model, or reliability of autonomy or human decision making.
Integrating High Level and Low Level Planning
Nov 26, 2016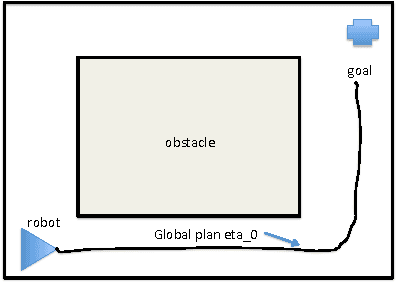
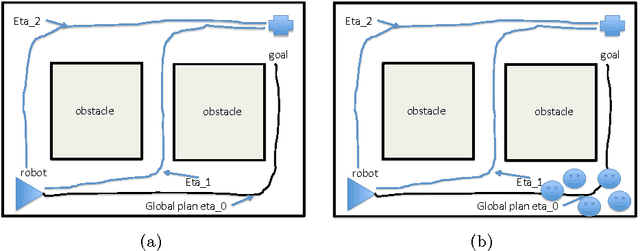
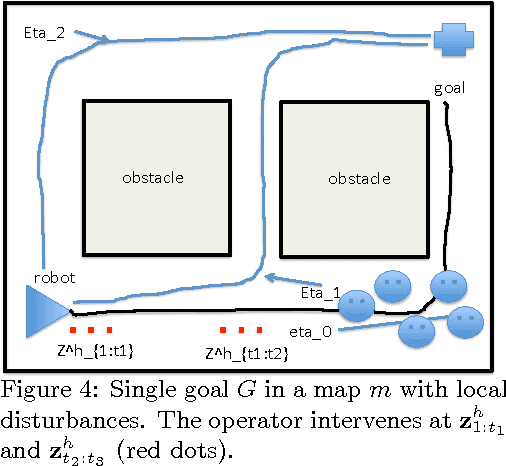
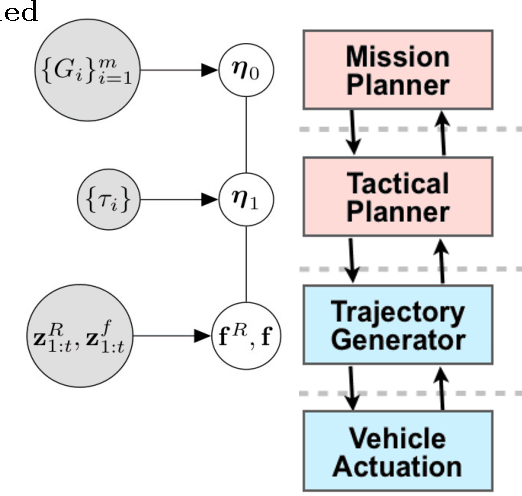
Abstract:We present a possible method for integrating high level and low level planning. To do so, we introduce the global plan random \emph{trajectory} $\boldsymbol{\eta}_0 \colon [1,T] \to \mathbb R^2$, measured by goals $G_i$ and governed by the distribution $p(\boldsymbol{\eta}_0 \mid \{ G_i\}_{i=1}^m)$. This distribution is combined with the low level robot-crowd planner $p(\mathbf{f}^{R},\mathbf{f}^{1},\ldots,\mathbf{f}^{n}\mid\mathbf{z}_{1:t})$ (from~\cite{trautmanicra2013, trautmaniros}) in the distribution $p(\boldsymbol{\eta}_0,\mathbf{f}^{(R)},\mathbf{f}\mid\mathbf{z}_{1:t})$. We explore this \emph{integrated planning} formulation in three case studies, and in the process find that this formulation 1) generalizes the ROS navigation stack in a practically useful way 2) arbitrates between high and low level decision making in a statistically sound manner when unanticipated local disturbances arise and 3) enables the integration of an onboard operator providing real time input at either the global (e.g., waypoint designation) or local (e.g., joystick) level. Importantly, the integrated planning formulation $p(\boldsymbol{\eta}_0,\mathbf{f}^{(R)},\mathbf{f}\mid\mathbf{z}_{1:t})$ highlights failure modes of the ROS navigation stack (and thus for standard hierarchical planning architectures); these failure modes are resolved by using $p(\boldsymbol{\eta}_0,\mathbf{f}^{(R)},\mathbf{f}\mid\mathbf{z}_{1:t})$. Finally, we conclude with a discussion of how results from formal methods can guide our factorization of $p(\boldsymbol{\eta}_0,\mathbf{f}^{(R)},\mathbf{f}\mid\mathbf{z}_{1:t})$.
Assistive Planning in Complex, Dynamic Environments: a Probabilistic Approach
Aug 06, 2015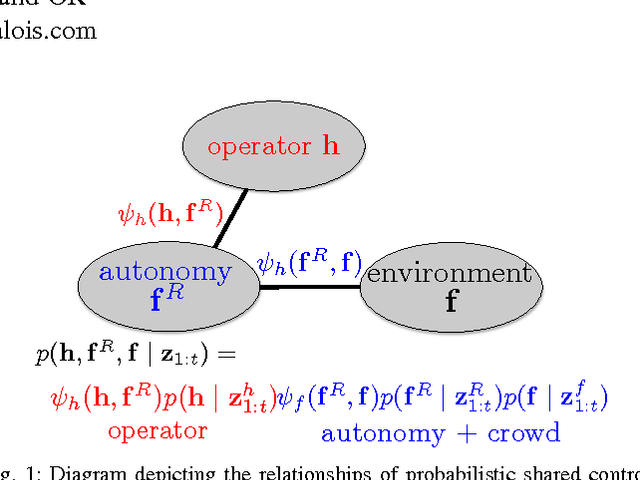
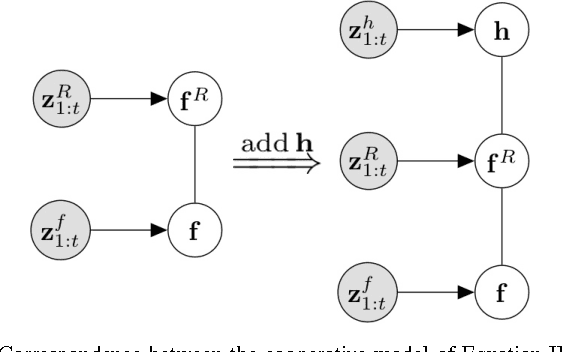
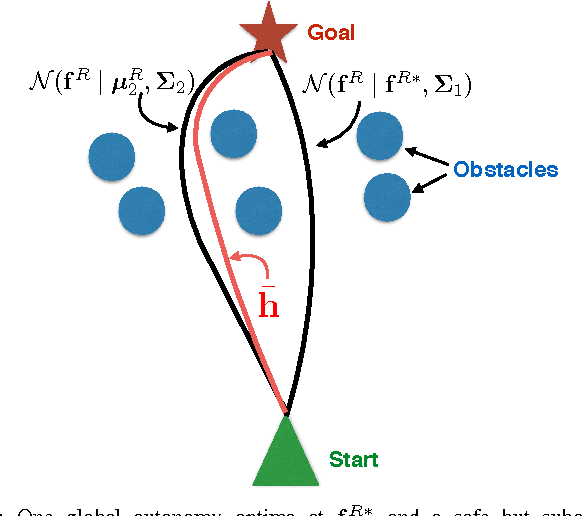

Abstract:We explore the probabilistic foundations of shared control in complex dynamic environments. In order to do this, we formulate shared control as a random process and describe the joint distribution that governs its behavior. For tractability, we model the relationships between the operator, autonomy, and crowd as an undirected graphical model. Further, we introduce an interaction function between the operator and the robot, that we call "agreeability"; in combination with the methods developed in~\cite{trautman-ijrr-2015}, we extend a cooperative collision avoidance autonomy to shared control. We therefore quantify the notion of simultaneously optimizing over agreeability (between the operator and autonomy), and safety and efficiency in crowded environments. We show that for a particular form of interaction function between the autonomy and the operator, linear blending is recovered exactly. Additionally, to recover linear blending, unimodal restrictions must be placed on the models describing the operator and the autonomy. In turn, these restrictions raise questions about the flexibility and applicability of the linear blending framework. Additionally, we present an extension of linear blending called "operator biased linear trajectory blending" (which formalizes some recent approaches in linear blending such as~\cite{dragan-ijrr-2013}) and show that not only is this also a restrictive special case of our probabilistic approach, but more importantly, is statistically unsound, and thus, mathematically, unsuitable for implementation. Instead, we suggest a statistically principled approach that guarantees data is used in a consistent manner, and show how this alternative approach converges to the full probabilistic framework. We conclude by proving that, in general, linear blending is suboptimal with respect to the joint metric of agreeability, safety, and efficiency.
A Unified Approach to 3 Basic Challenges in Shared Autonomy
Aug 06, 2015Abstract:We discuss some of the challenges facing shared autonomy. In particular, we explore 1) shared autonomy over unreliable networks, 2) how we can model individual human operators (in contrast to the average of a human operator), and 3) how our approach naturally models and integrates sliding autonomy into the joint human-machine system. We include a Background Section for completeness.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge