Sparse Interacting Gaussian Processes: Efficiency and Optimality Theorems of Autonomous Crowd Navigation
Paper and Code
May 10, 2017


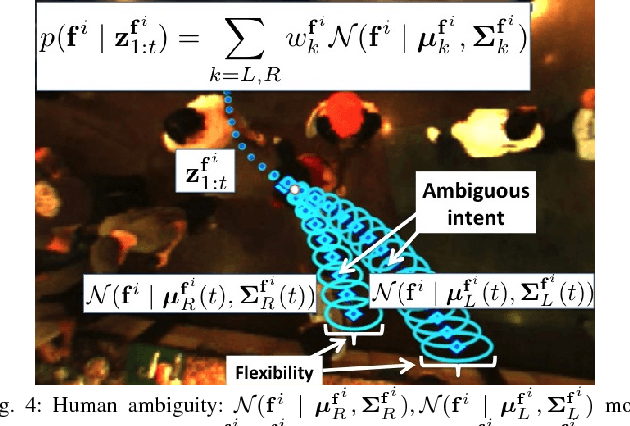
We study the sparsity and optimality properties of crowd navigation and find that existing techniques do not satisfy both criteria simultaneously: either they achieve optimality with a prohibitive number of samples or tractability assumptions make them fragile to catastrophe. For example, if the human and robot are modeled independently, then tractability is attained but the planner is prone to overcautious or overaggressive behavior. For sampling based motion planning of joint human-robot cost functions, for $n_t$ agents and $T$ step lookahead, $\mathcal O(2^{2n_t T})$ samples are needed for coverage of the action space. Advanced approaches statically partition the action space into free-space and then sample in those convex regions. However, if the human is \emph{moving} into free-space, then the partition is misleading and sampling is unsafe: free space will soon be occupied. We diagnose the cause of these deficiencies---optimization happens over \emph{trajectory} space---and propose a novel solution: optimize over trajectory \emph{distribution} space by using a Gaussian process (GP) basis. We exploit the "kernel trick" of GPs, where a continuum of trajectories are captured with a mean and covariance function. By using the mean and covariance as proxies for a trajectory family we reason about collective trajectory behavior without resorting to sampling. The GP basis is sparse and optimal with respect to collision avoidance and robot and crowd intention and flexibility. GP sparsity leans heavily on the insight that joint action space decomposes into free regions; however, the decomposition contains feasible solutions only if the partition is dynamically generated. We call our approach \emph{$\mathcal O(2^{n_t})$-sparse interacting Gaussian processes}.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge