Integrating High Level and Low Level Planning
Paper and Code
Nov 26, 2016

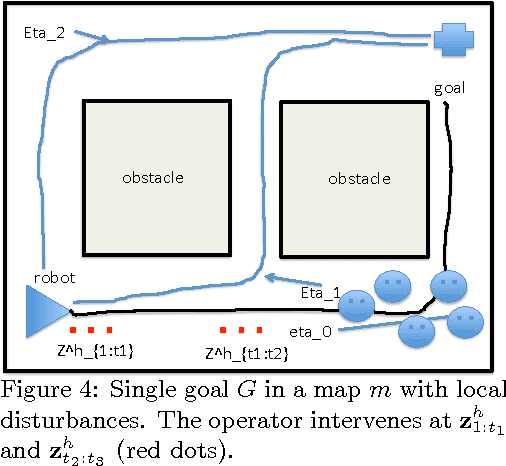
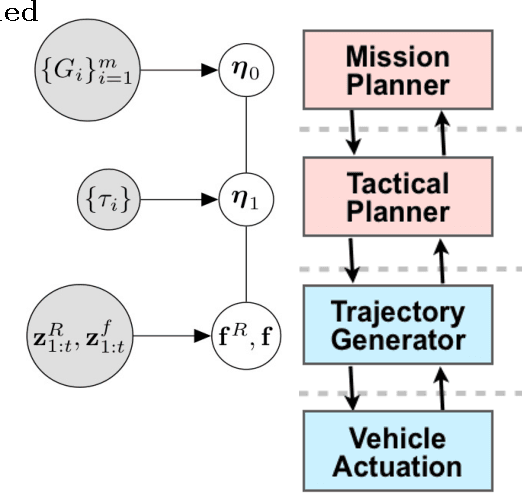
We present a possible method for integrating high level and low level planning. To do so, we introduce the global plan random \emph{trajectory} $\boldsymbol{\eta}_0 \colon [1,T] \to \mathbb R^2$, measured by goals $G_i$ and governed by the distribution $p(\boldsymbol{\eta}_0 \mid \{ G_i\}_{i=1}^m)$. This distribution is combined with the low level robot-crowd planner $p(\mathbf{f}^{R},\mathbf{f}^{1},\ldots,\mathbf{f}^{n}\mid\mathbf{z}_{1:t})$ (from~\cite{trautmanicra2013, trautmaniros}) in the distribution $p(\boldsymbol{\eta}_0,\mathbf{f}^{(R)},\mathbf{f}\mid\mathbf{z}_{1:t})$. We explore this \emph{integrated planning} formulation in three case studies, and in the process find that this formulation 1) generalizes the ROS navigation stack in a practically useful way 2) arbitrates between high and low level decision making in a statistically sound manner when unanticipated local disturbances arise and 3) enables the integration of an onboard operator providing real time input at either the global (e.g., waypoint designation) or local (e.g., joystick) level. Importantly, the integrated planning formulation $p(\boldsymbol{\eta}_0,\mathbf{f}^{(R)},\mathbf{f}\mid\mathbf{z}_{1:t})$ highlights failure modes of the ROS navigation stack (and thus for standard hierarchical planning architectures); these failure modes are resolved by using $p(\boldsymbol{\eta}_0,\mathbf{f}^{(R)},\mathbf{f}\mid\mathbf{z}_{1:t})$. Finally, we conclude with a discussion of how results from formal methods can guide our factorization of $p(\boldsymbol{\eta}_0,\mathbf{f}^{(R)},\mathbf{f}\mid\mathbf{z}_{1:t})$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge