Assistive Planning in Complex, Dynamic Environments: a Probabilistic Approach
Paper and Code
Aug 06, 2015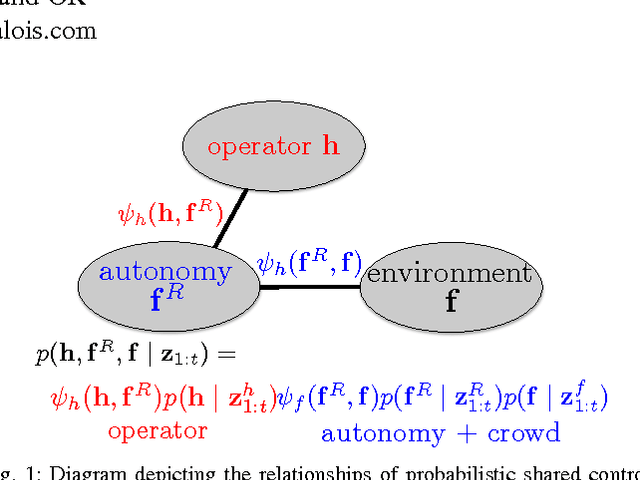



We explore the probabilistic foundations of shared control in complex dynamic environments. In order to do this, we formulate shared control as a random process and describe the joint distribution that governs its behavior. For tractability, we model the relationships between the operator, autonomy, and crowd as an undirected graphical model. Further, we introduce an interaction function between the operator and the robot, that we call "agreeability"; in combination with the methods developed in~\cite{trautman-ijrr-2015}, we extend a cooperative collision avoidance autonomy to shared control. We therefore quantify the notion of simultaneously optimizing over agreeability (between the operator and autonomy), and safety and efficiency in crowded environments. We show that for a particular form of interaction function between the autonomy and the operator, linear blending is recovered exactly. Additionally, to recover linear blending, unimodal restrictions must be placed on the models describing the operator and the autonomy. In turn, these restrictions raise questions about the flexibility and applicability of the linear blending framework. Additionally, we present an extension of linear blending called "operator biased linear trajectory blending" (which formalizes some recent approaches in linear blending such as~\cite{dragan-ijrr-2013}) and show that not only is this also a restrictive special case of our probabilistic approach, but more importantly, is statistically unsound, and thus, mathematically, unsuitable for implementation. Instead, we suggest a statistically principled approach that guarantees data is used in a consistent manner, and show how this alternative approach converges to the full probabilistic framework. We conclude by proving that, in general, linear blending is suboptimal with respect to the joint metric of agreeability, safety, and efficiency.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge