Derivative-Based Koopman Operators for Real-Time Control of Robotic Systems
Paper and Code
Oct 12, 2020
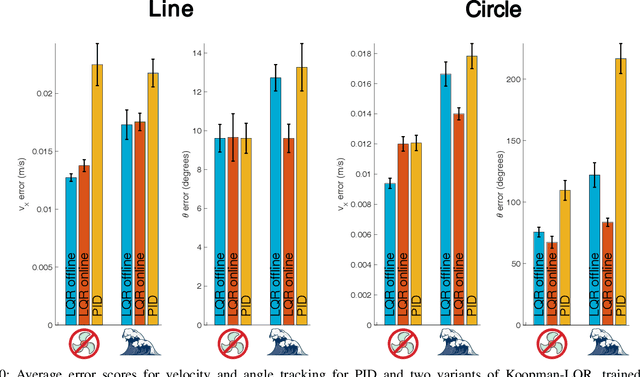


This paper presents a methodology for linear embedding of nonlinear systems that bounds the model error in terms of the prediction horizon and the magnitude of the derivatives of the system states. Using higher-order derivatives of general nonlinear dynamics that need not be known, we construct a Koopman operator-based linear representation and utilize Taylor series accuracy to derive an error bound. The error formula is used to choose the order of derivatives in the basis functions and obtain a data-driven Koopman model using a closed-form expression that can be computed in real time. The Koopman representation of the nonlinear system is then used to synthesize LQR feedback. The efficacy of the embedding approach is demonstrated with simulation and experimental results on the control of a tail-actuated robotic fish. Experimental results show that the proposed data-driven control approach outperforms a tuned PID (Proportional Integral Derivative) controller and that updating the data-driven model online significantly improves performance in the presence of unmodeled fluid disturbance. This paper is complemented with a video: https://youtu.be/9_wx0tdDta0.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge