Top-Down Knowledge Compilation for Counting Modulo Theories

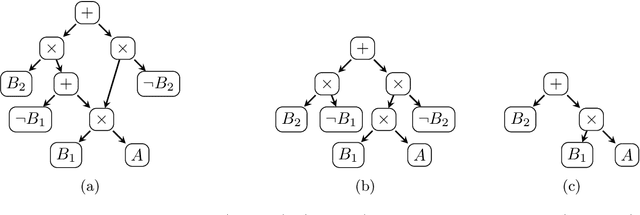
Propositional model counting (#SAT) can be solved efficiently when the input formula is in deterministic decomposable negation normal form (d-DNNF). Translating an arbitrary formula into a representation that allows inference tasks, such as counting, to be performed efficiently, is called knowledge compilation. Top-down knowledge compilation is a state-of-the-art technique for solving #SAT problems that leverages the traces of exhaustive DPLL search to obtain d-DNNF representations. While knowledge compilation is well studied for propositional approaches, knowledge compilation for the (quantifier free) counting modulo theory setting (#SMT) has been studied to a much lesser degree. In this paper, we discuss compilation strategies for #SMT. We specifically advocate for a top-down compiler based on the traces of exhaustive DPLL(T) search.

Learning MAX-SAT from Contextual Examples for Combinatorial Optimisation

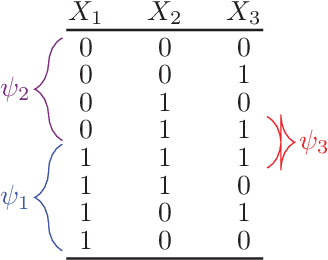
Combinatorial optimisation problems are ubiquitous in artificial intelligence. Designing the underlying models, however, requires substantial expertise, which is a limiting factor in practice. The models typically consist of hard and soft constraints, or combine hard constraints with an objective function. We introduce a novel setting for learning combinatorial optimisation problems from contextual examples. These positive and negative examples show - in a particular context - whether the solutions are good enough or not. We develop our framework using the MAX-SAT formalism as it is simple yet powerful setting having these features. We study the learnability of MAX-SAT models. Our theoretical results show that high-quality MAX-SAT models can be learned from contextual examples in the realisable and agnostic settings, as long as the data satisfies an intuitive "representativeness" condition. We also contribute two implementations based on our theoretical results: one leverages ideas from syntax-guided synthesis while the other makes use of stochastic local search techniques. The two implementations are evaluated by recovering synthetic and benchmark models from contextual examples. The experimental results support our theoretical analysis, showing that MAX-SAT models can be learned from contextual examples. Among the two implementations, the stochastic local search learner scales much better than the syntax-guided implementation while providing comparable or better models.

Learning Mixed-Integer Linear Programs from Contextual Examples

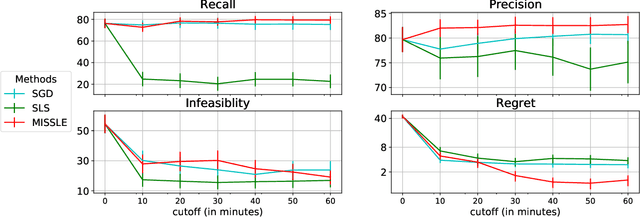
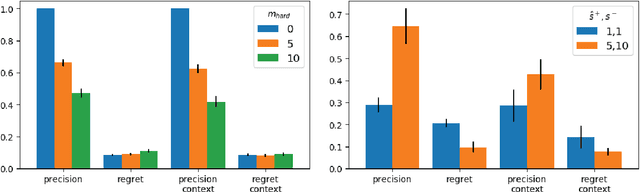
Mixed-integer linear programs (MILPs) are widely used in artificial intelligence and operations research to model complex decision problems like scheduling and routing. Designing such programs however requires both domain and modelling expertise. In this paper, we study the problem of acquiring MILPs from contextual examples, a novel and realistic setting in which examples capture solutions and non-solutions within a specific context. The resulting learning problem involves acquiring continuous parameters -- namely, a cost vector and a feasibility polytope -- but has a distinctly combinatorial flavor. To solve this complex problem, we also contribute MISSLE, an algorithm for learning MILPs from contextual examples. MISSLE uses a variant of stochastic local search that is guided by the gradient of a continuous surrogate loss function. Our empirical evaluation on synthetic data shows that MISSLE acquires better MILPs faster than alternatives based on stochastic local search and gradient descent.

Human-Machine Collaboration for Democratizing Data Science

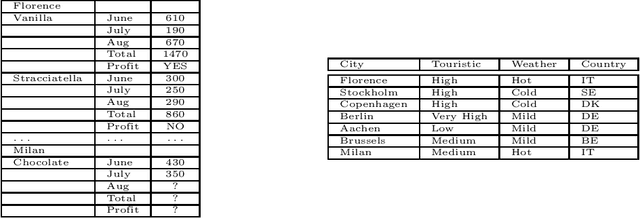
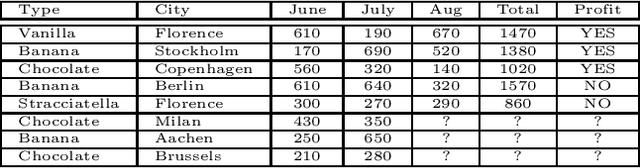
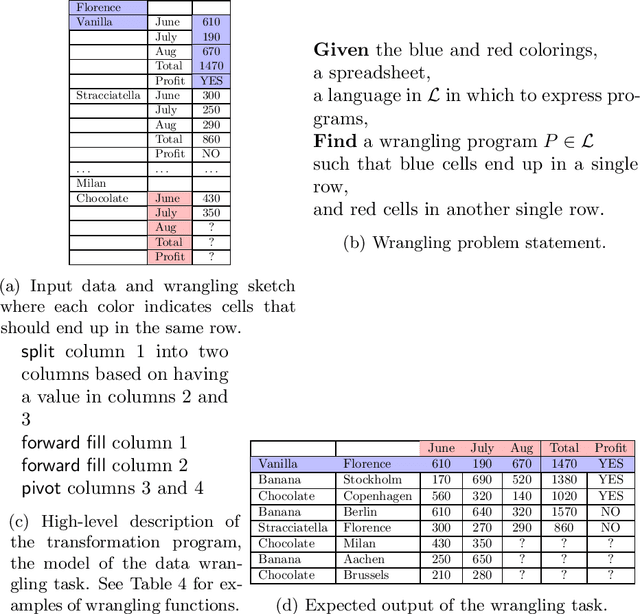
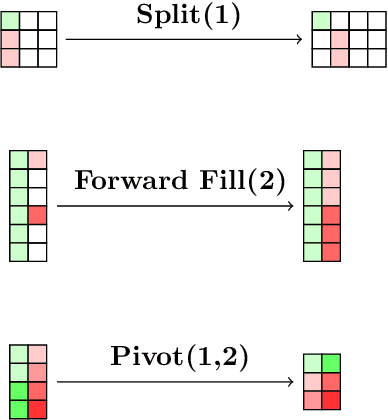
Everybody wants to analyse their data, but only few posses the data science expertise to to this. Motivated by this observation we introduce a novel framework and system \textsc{VisualSynth} for human-machine collaboration in data science. It wants to democratize data science by allowing users to interact with standard spreadsheet software in order to perform and automate various data analysis tasks ranging from data wrangling, data selection, clustering, constraint learning, predictive modeling and auto-completion. \textsc{VisualSynth} relies on the user providing colored sketches, i.e., coloring parts of the spreadsheet, to partially specify data science tasks, which are then determined and executed using artificial intelligence techniques.

Monte Carlo Anti-Differentiation for Approximate Weighted Model Integration

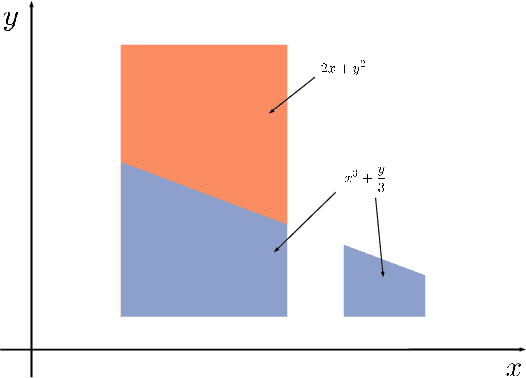
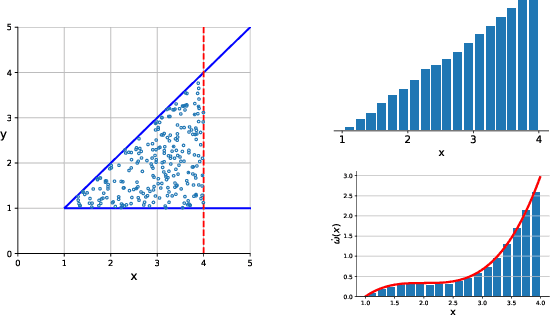
Probabilistic inference in the hybrid domain, i.e. inference over discrete-continuous domains, requires tackling two well known #P-hard problems 1)~weighted model counting (WMC) over discrete variables and 2)~integration over continuous variables. For both of these problems inference techniques have been developed separately in order to manage their #P-hardness, such as knowledge compilation for WMC and Monte Carlo (MC) methods for (approximate) integration in the continuous domain. Weighted model integration (WMI), the extension of WMC to the hybrid domain, has been proposed as a formalism to study probabilistic inference over discrete and continuous variables alike. Recently developed WMI solvers have focused on exploiting structure in WMI problems, for which they rely on symbolic integration to find the primitive of an integrand, i.e. to perform anti-differentiation. To combine these advances with state-of-the-art Monte Carlo integration techniques, we introduce \textit{Monte Carlo anti-differentiation} (MCAD), which computes MC approximations of anti-derivatives. In our empirical evaluation we substitute the exact symbolic integration backend in an existing WMI solver with an MCAD backend. Our experiments show that that equipping existing WMI solvers with MCAD yields a fast yet reliable approximate inference scheme.