IFH: a Diffusion Framework for Flexible Design of Graph Generative Models

Graph generative models can be classified into two prominent families: one-shot models, which generate a graph in one go, and sequential models, which generate a graph by successive additions of nodes and edges. Ideally, between these two extreme models lies a continuous range of models that adopt different levels of sequentiality. This paper proposes a graph generative model, called Insert-Fill-Halt (IFH), that supports the specification of a sequentiality degree. IFH is based upon the theory of Denoising Diffusion Probabilistic Models (DDPM), designing a node removal process that gradually destroys a graph. An insertion process learns to reverse this removal process by inserting arcs and nodes according to the specified sequentiality degree. We evaluate the performance of IFH in terms of quality, run time, and memory, depending on different sequentiality degrees. We also show that using DiGress, a diffusion-based one-shot model, as a generative step in IFH leads to improvement to the model itself, and is competitive with the current state-of-the-art.

Transformers discover an elementary calculation system exploiting local attention and grid-like problem representation

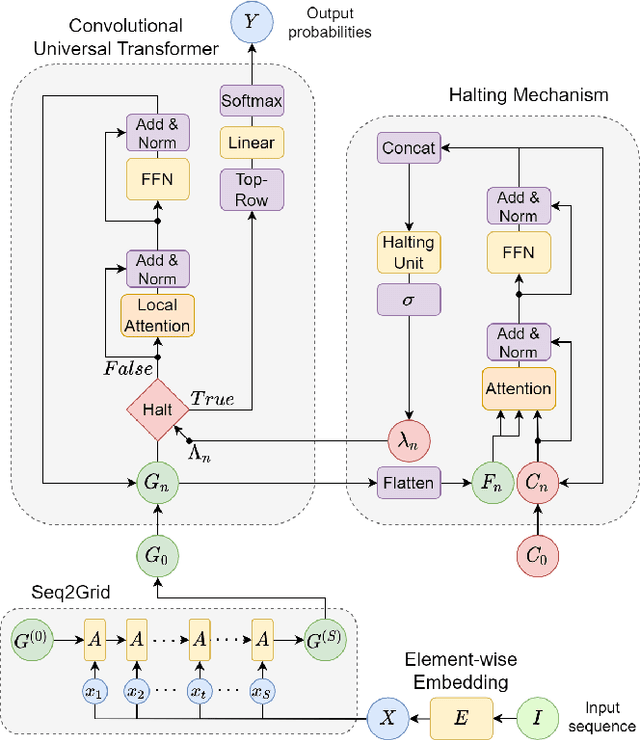
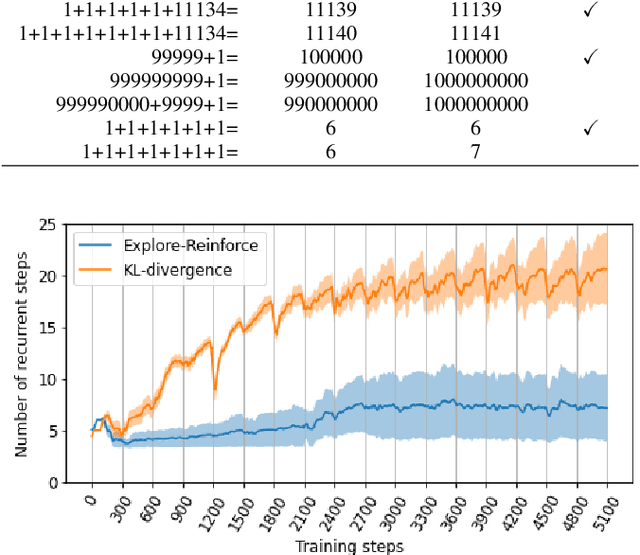
Mathematical reasoning is one of the most impressive achievements of human intellect but remains a formidable challenge for artificial intelligence systems. In this work we explore whether modern deep learning architectures can learn to solve a symbolic addition task by discovering effective arithmetic procedures. Although the problem might seem trivial at first glance, generalizing arithmetic knowledge to operations involving a higher number of terms, possibly composed by longer sequences of digits, has proven extremely challenging for neural networks. Here we show that universal transformers equipped with local attention and adaptive halting mechanisms can learn to exploit an external, grid-like memory to carry out multi-digit addition. The proposed model achieves remarkable accuracy even when tested with problems requiring extrapolation outside the training distribution; most notably, it does so by discovering human-like calculation strategies such as place value alignment.