Every Model Learned by Gradient Descent Is Approximately a Kernel Machine

Deep learning's successes are often attributed to its ability to automatically discover new representations of the data, rather than relying on handcrafted features like other learning methods. We show, however, that deep networks learned by the standard gradient descent algorithm are in fact mathematically approximately equivalent to kernel machines, a learning method that simply memorizes the data and uses it directly for prediction via a similarity function (the kernel). This greatly enhances the interpretability of deep network weights, by elucidating that they are effectively a superposition of the training examples. The network architecture incorporates knowledge of the target function into the kernel. This improved understanding should lead to better learning algorithms.

Amodal 3D Reconstruction for Robotic Manipulation via Stability and Connectivity

Learning-based 3D object reconstruction enables single- or few-shot estimation of 3D object models. For robotics, this holds the potential to allow model-based methods to rapidly adapt to novel objects and scenes. Existing 3D reconstruction techniques optimize for visual reconstruction fidelity, typically measured by chamfer distance or voxel IOU. We find that when applied to realistic, cluttered robotics environments, these systems produce reconstructions with low physical realism, resulting in poor task performance when used for model-based control. We propose ARM, an amodal 3D reconstruction system that introduces (1) a stability prior over object shapes, (2) a connectivity prior, and (3) a multi-channel input representation that allows for reasoning over relationships between groups of objects. By using these priors over the physical properties of objects, our system improves reconstruction quality not just by standard visual metrics, but also performance of model-based control on a variety of robotics manipulation tasks in challenging, cluttered environments. Code is available at github.com/wagnew3/ARM.

Self-Supervised Object-Level Deep Reinforcement Learning

Current deep reinforcement learning approaches incorporate minimal prior knowledge about the environment, limiting computational and sample efficiency. We incorporate a few object-based priors that humans are known to use: "Infants divide perceptual arrays into units that move as connected wholes, that move separately from one another, that tend to maintain their size and shape over motion, and that tend to act upon each other only on contact" [Spelke]. We propose a probabilistic object-based model of environments and use human object priors to develop an efficient self-supervised algorithm for maximum likelihood estimation of the model parameters from observations and for inferring objects directly from the perceptual stream. We then use object features and incorporate object-contact priors to improve the sample efficiency our object-based RL agent.We evaluate our approach on a subset of the Atari benchmarks, and learn up to four orders of magnitude faster than the standard deep Q-learning network, rendering rapid desktop experiments in this domain feasible. To our knowledge, our system is the first to learn any Atari task in fewer environment interactions than humans.

Deep Learning as a Mixed Convex-Combinatorial Optimization Problem

As neural networks grow deeper and wider, learning networks with hard-threshold activations is becoming increasingly important, both for network quantization, which can drastically reduce time and energy requirements, and for creating large integrated systems of deep networks, which may have non-differentiable components and must avoid vanishing and exploding gradients for effective learning. However, since gradient descent is not applicable to hard-threshold functions, it is not clear how to learn networks of them in a principled way. We address this problem by observing that setting targets for hard-threshold hidden units in order to minimize loss is a discrete optimization problem, and can be solved as such. The discrete optimization goal is to find a set of targets such that each unit, including the output, has a linearly separable problem to solve. Given these targets, the network decomposes into individual perceptrons, which can then be learned with standard convex approaches. Based on this, we develop a recursive mini-batch algorithm for learning deep hard-threshold networks that includes the popular but poorly justified straight-through estimator as a special case. Empirically, we show that our algorithm improves classification accuracy in a number of settings, including for AlexNet and ResNet-18 on ImageNet, when compared to the straight-through estimator.

Neural-Symbolic Learning and Reasoning: A Survey and Interpretation

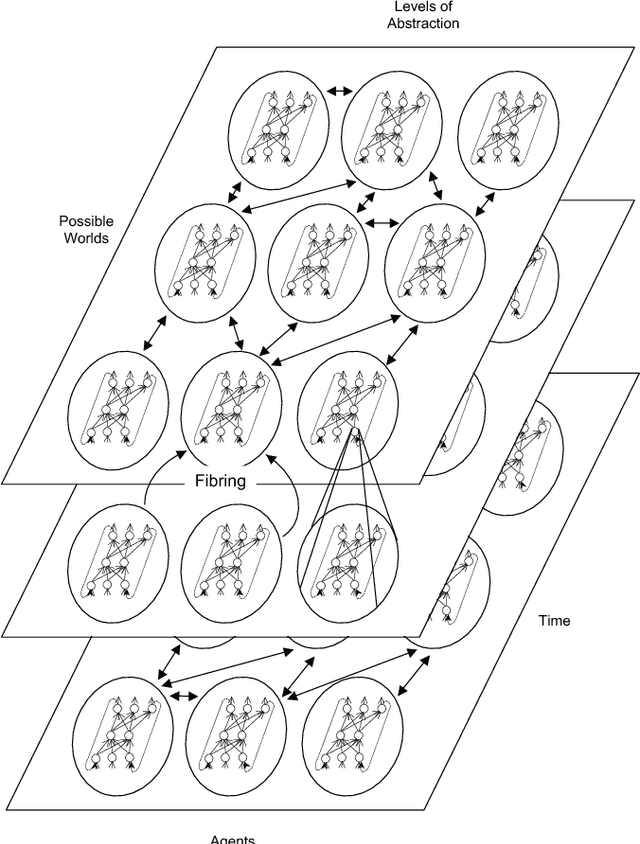
The study and understanding of human behaviour is relevant to computer science, artificial intelligence, neural computation, cognitive science, philosophy, psychology, and several other areas. Presupposing cognition as basis of behaviour, among the most prominent tools in the modelling of behaviour are computational-logic systems, connectionist models of cognition, and models of uncertainty. Recent studies in cognitive science, artificial intelligence, and psychology have produced a number of cognitive models of reasoning, learning, and language that are underpinned by computation. In addition, efforts in computer science research have led to the development of cognitive computational systems integrating machine learning and automated reasoning. Such systems have shown promise in a range of applications, including computational biology, fault diagnosis, training and assessment in simulators, and software verification. This joint survey reviews the personal ideas and views of several researchers on neural-symbolic learning and reasoning. The article is organised in three parts: Firstly, we frame the scope and goals of neural-symbolic computation and have a look at the theoretical foundations. We then proceed to describe the realisations of neural-symbolic computation, systems, and applications. Finally we present the challenges facing the area and avenues for further research.

The Sum-Product Theorem: A Foundation for Learning Tractable Models

Inference in expressive probabilistic models is generally intractable, which makes them difficult to learn and limits their applicability. Sum-product networks are a class of deep models where, surprisingly, inference remains tractable even when an arbitrary number of hidden layers are present. In this paper, we generalize this result to a much broader set of learning problems: all those where inference consists of summing a function over a semiring. This includes satisfiability, constraint satisfaction, optimization, integration, and others. In any semiring, for summation to be tractable it suffices that the factors of every product have disjoint scopes. This unifies and extends many previous results in the literature. Enforcing this condition at learning time thus ensures that the learned models are tractable. We illustrate the power and generality of this approach by applying it to a new type of structured prediction problem: learning a nonconvex function that can be globally optimized in polynomial time. We show empirically that this greatly outperforms the standard approach of learning without regard to the cost of optimization.

Recursive Decomposition for Nonconvex Optimization

Continuous optimization is an important problem in many areas of AI, including vision, robotics, probabilistic inference, and machine learning. Unfortunately, most real-world optimization problems are nonconvex, causing standard convex techniques to find only local optima, even with extensions like random restarts and simulated annealing. We observe that, in many cases, the local modes of the objective function have combinatorial structure, and thus ideas from combinatorial optimization can be brought to bear. Based on this, we propose a problem-decomposition approach to nonconvex optimization. Similarly to DPLL-style SAT solvers and recursive conditioning in probabilistic inference, our algorithm, RDIS, recursively sets variables so as to simplify and decompose the objective function into approximately independent sub-functions, until the remaining functions are simple enough to be optimized by standard techniques like gradient descent. The variables to set are chosen by graph partitioning, ensuring decomposition whenever possible. We show analytically that RDIS can solve a broad class of nonconvex optimization problems exponentially faster than gradient descent with random restarts. Experimentally, RDIS outperforms standard techniques on problems like structure from motion and protein folding.

On the Latent Variable Interpretation in Sum-Product Networks

One of the central themes in Sum-Product networks (SPNs) is the interpretation of sum nodes as marginalized latent variables (LVs). This interpretation yields an increased syntactic or semantic structure, allows the application of the EM algorithm and to efficiently perform MPE inference. In literature, the LV interpretation was justified by explicitly introducing the indicator variables corresponding to the LVs' states. However, as pointed out in this paper, this approach is in conflict with the completeness condition in SPNs and does not fully specify the probabilistic model. We propose a remedy for this problem by modifying the original approach for introducing the LVs, which we call SPN augmentation. We discuss conditional independencies in augmented SPNs, formally establish the probabilistic interpretation of the sum-weights and give an interpretation of augmented SPNs as Bayesian networks. Based on these results, we find a sound derivation of the EM algorithm for SPNs. Furthermore, the Viterbi-style algorithm for MPE proposed in literature was never proven to be correct. We show that this is indeed a correct algorithm, when applied to selective SPNs, and in particular when applied to augmented SPNs. Our theoretical results are confirmed in experiments on synthetic data and 103 real-world datasets.

Learning Tractable Probabilistic Models for Fault Localization

In recent years, several probabilistic techniques have been applied to various debugging problems. However, most existing probabilistic debugging systems use relatively simple statistical models, and fail to generalize across multiple programs. In this work, we propose Tractable Fault Localization Models (TFLMs) that can be learned from data, and probabilistically infer the location of the bug. While most previous statistical debugging methods generalize over many executions of a single program, TFLMs are trained on a corpus of previously seen buggy programs, and learn to identify recurring patterns of bugs. Widely-used fault localization techniques such as TARANTULA evaluate the suspiciousness of each line in isolation; in contrast, a TFLM defines a joint probability distribution over buggy indicator variables for each line. Joint distributions with rich dependency structure are often computationally intractable; TFLMs avoid this by exploiting recent developments in tractable probabilistic models (specifically, Relational SPNs). Further, TFLMs can incorporate additional sources of information, including coverage-based features such as TARANTULA. We evaluate the fault localization performance of TFLMs that include TARANTULA scores as features in the probabilistic model. Our study shows that the learned TFLMs isolate bugs more effectively than previous statistical methods or using TARANTULA directly.

Exchangeable Variable Models

A sequence of random variables is exchangeable if its joint distribution is invariant under variable permutations. We introduce exchangeable variable models (EVMs) as a novel class of probabilistic models whose basic building blocks are partially exchangeable sequences, a generalization of exchangeable sequences. We prove that a family of tractable EVMs is optimal under zero-one loss for a large class of functions, including parity and threshold functions, and strictly subsumes existing tractable independence-based model families. Extensive experiments show that EVMs outperform state of the art classifiers such as SVMs and probabilistic models which are solely based on independence assumptions.