Discrete and Continuous Deep Residual Learning Over Graphs
Paper and Code
Nov 26, 2019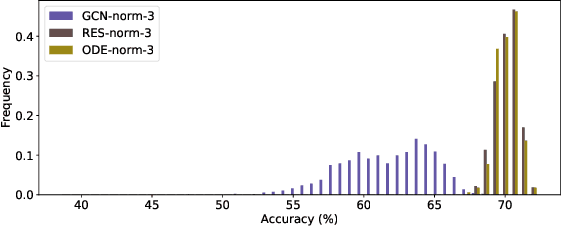
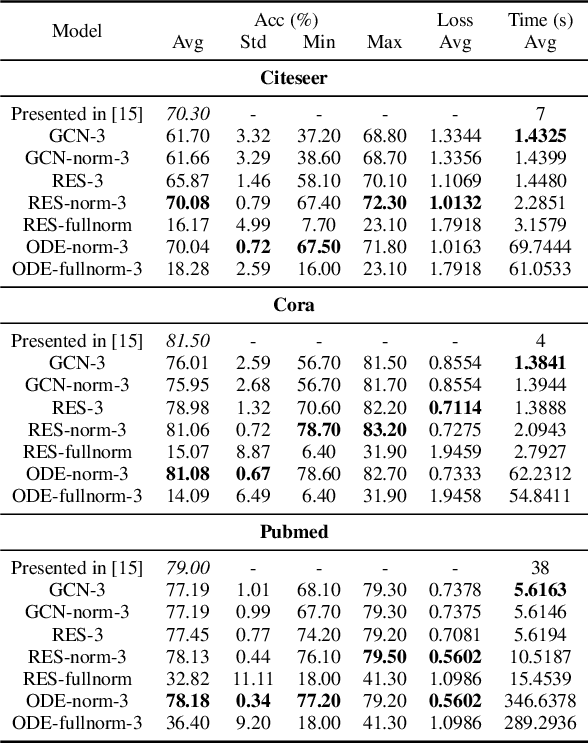
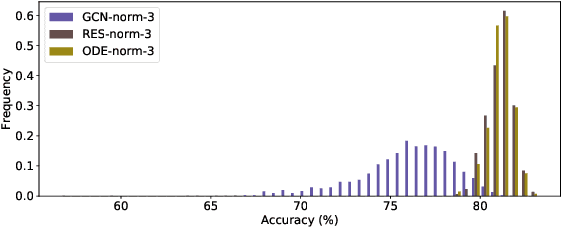
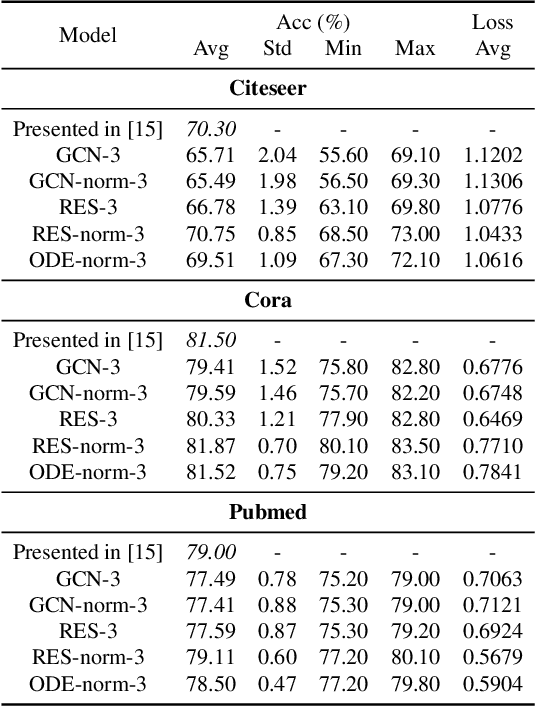
In this paper we propose the use of continuous residual modules for graph kernels in Graph Neural Networks. We show how both discrete and continuous residual layers allow for more robust training, being that continuous residual layers are those which are applied by integrating through an Ordinary Differential Equation (ODE) solver to produce their output. We experimentally show that these residuals achieve better results than the ones with non-residual modules when multiple layers are used, mitigating the low-pass filtering effect of GCN-based models. Finally, we apply and analyse the behaviour of these techniques and give pointers to how this technique can be useful in other domains by allowing more predictable behaviour under dynamic times of computation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge