Relational Graph Convolutional Networks Do Not Learn Sound Rules

Graph neural networks (GNNs) are frequently used to predict missing facts in knowledge graphs (KGs). Motivated by the lack of explainability for the outputs of these models, recent work has aimed to explain their predictions using Datalog, a widely used logic-based formalism. However, such work has been restricted to certain subclasses of GNNs. In this paper, we consider one of the most popular GNN architectures for KGs, R-GCN, and we provide two methods to extract rules that explain its predictions and are sound, in the sense that each fact derived by the rules is also predicted by the GNN, for any input dataset. Furthermore, we provide a method that can verify that certain classes of Datalog rules are not sound for the R-GCN. In our experiments, we train R-GCNs on KG completion benchmarks, and we are able to verify that no Datalog rule is sound for these models, even though the models often obtain high to near-perfect accuracy. This raises some concerns about the ability of R-GCN models to generalise and about the explainability of their predictions. We further provide two variations to the training paradigm of R-GCN that encourage it to learn sound rules and find a trade-off between model accuracy and the number of learned sound rules.

On the Correspondence Between Monotonic Max-Sum GNNs and Datalog

Although there has been significant interest in applying machine learning techniques to structured data, the expressivity (i.e., a description of what can be learned) of such techniques is still poorly understood. In this paper, we study data transformations based on graph neural networks (GNNs). First, we note that the choice of how a dataset is encoded into a numeric form processable by a GNN can obscure the characterisation of a model's expressivity, and we argue that a canonical encoding provides an appropriate basis. Second, we study the expressivity of monotonic max-sum GNNs, which cover a subclass of GNNs with max and sum aggregation functions. We show that, for each such GNN, one can compute a Datalog program such that applying the GNN to any dataset produces the same facts as a single round of application of the program's rules to the dataset. Monotonic max-sum GNNs can sum an unbounded number of feature vectors which can result in arbitrarily large feature values, whereas rule application requires only a bounded number of constants. Hence, our result shows that the unbounded summation of monotonic max-sum GNNs does not increase their expressive power. Third, we sharpen our result to the subclass of monotonic max GNNs, which use only the max aggregation function, and identify a corresponding class of Datalog programs.

Revisiting Inferential Benchmarks for Knowledge Graph Completion

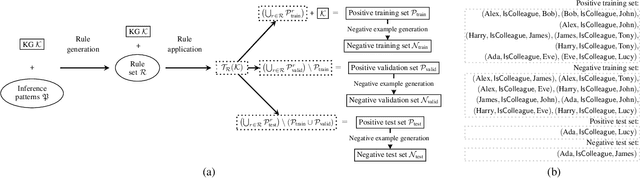
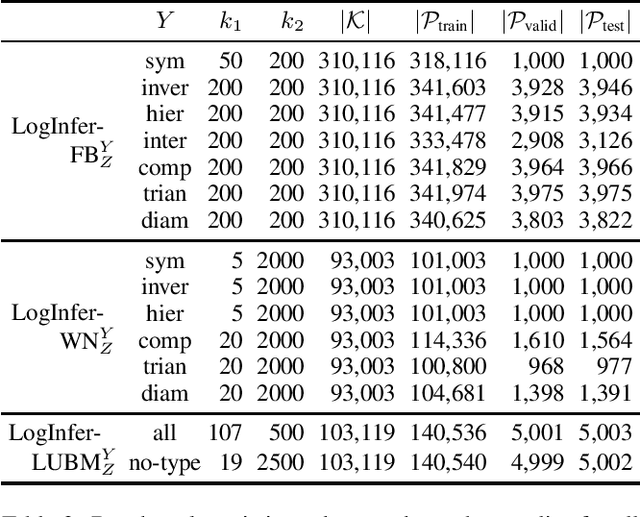
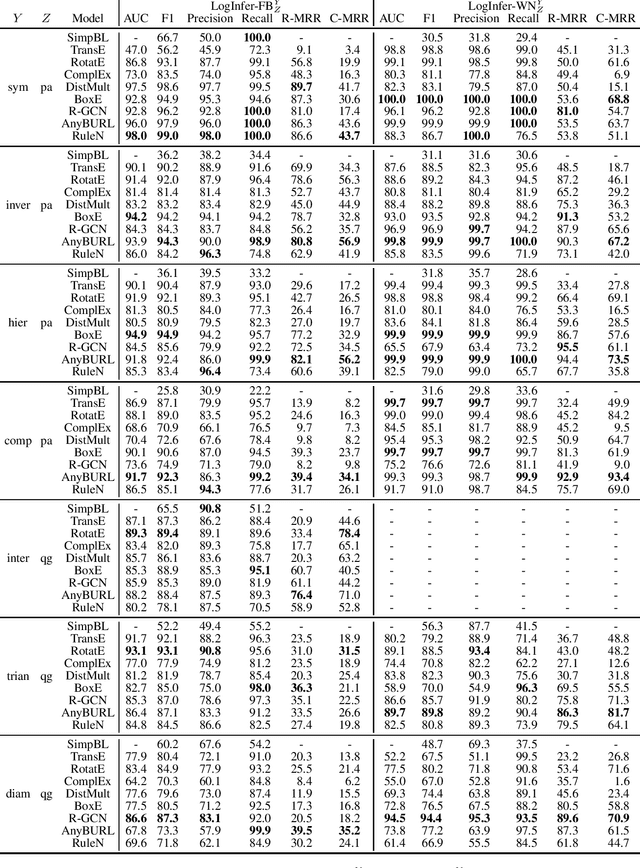
Knowledge Graph (KG) completion is the problem of extending an incomplete KG with missing facts. A key feature of Machine Learning approaches for KG completion is their ability to learn inference patterns, so that the predicted facts are the results of applying these patterns to the KG. Standard completion benchmarks, however, are not well-suited for evaluating models' abilities to learn patterns, because the training and test sets of these benchmarks are a random split of a given KG and hence do not capture the causality of inference patterns. We propose a novel approach for designing KG completion benchmarks based on the following principles: there is a set of logical rules so that the missing facts are the results of the rules' application; the training set includes both premises matching rule antecedents and the corresponding conclusions; the test set consists of the results of applying the rules to the training set; the negative examples are designed to discourage the models from learning rules not entailed by the rule set. We use our methodology to generate several benchmarks and evaluate a wide range of existing KG completion systems. Our results provide novel insights on the ability of existing models to induce inference patterns from incomplete KGs.

Seminaive Materialisation in DatalogMTL

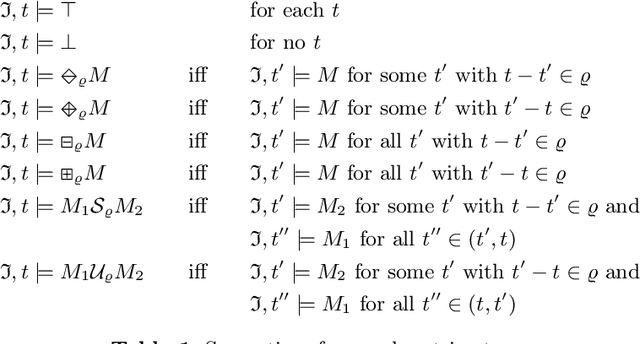
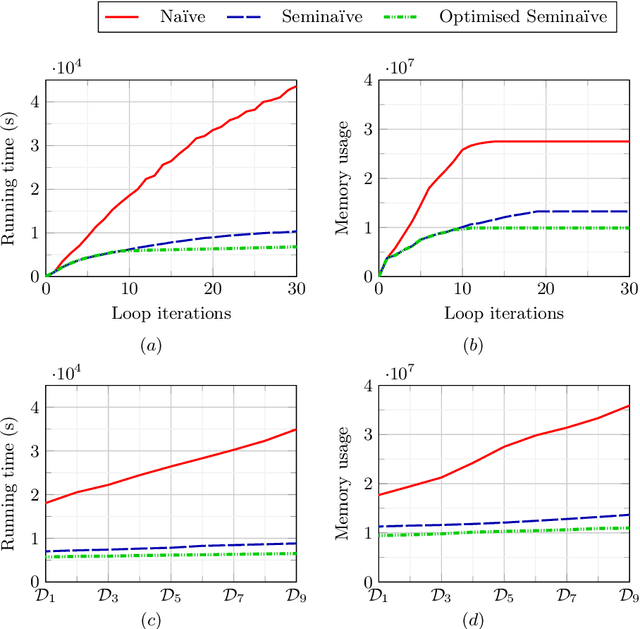
DatalogMTL is an extension of Datalog with metric temporal operators that has found applications in temporal ontology-based data access and query answering, as well as in stream reasoning. Practical algorithms for DatalogMTL are reliant on materialisation-based reasoning, where temporal facts are derived in a forward chaining manner in successive rounds of rule applications. Current materialisation-based procedures are, however, based on a naive evaluation strategy, where the main source of inefficiency stems from redundant computations. In this paper, we propose a materialisation-based procedure which, analogously to the classical seminaive algorithm in Datalog, aims at minimising redundant computation by ensuring that each temporal rule instance is considered at most once during the execution of the algorithm. Our experiments show that our optimised seminaive strategy for DatalogMTL is able to significantly reduce materialisation times.

Augmenting Message Passing by Retrieving Similar Graphs

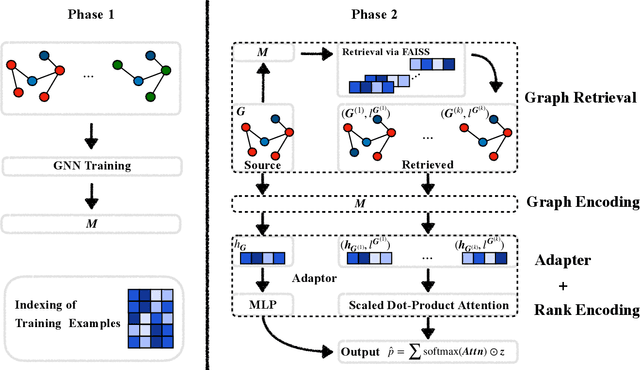
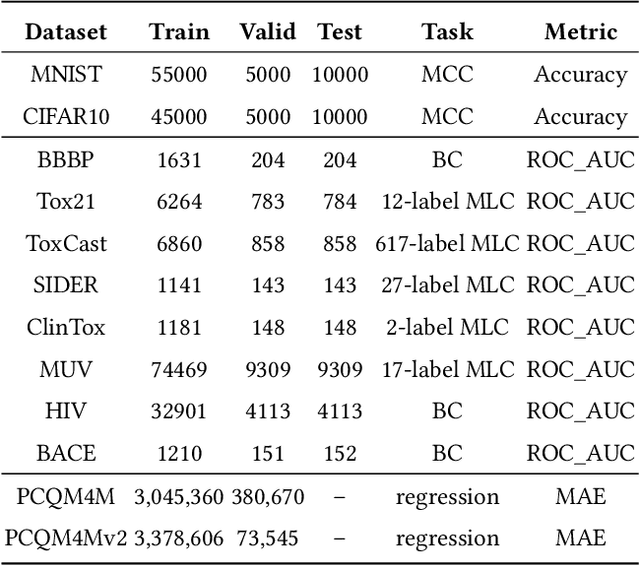
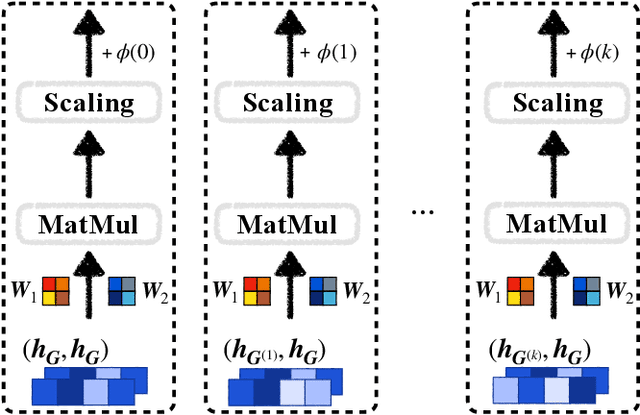
Graph Neural Networks (GNNs) are effective tools for graph representation learning. Most GNNs rely on a recursive neighborhood aggregation scheme, named message passing. In this paper, motivated by the success of retrieval-based models, we propose a non-parametric scheme called GraphRetrieval, in which similar training graphs associated with their ground-truth labels are retrieved to be jointly utilized with the input graph representation to complete various graph-based predictive tasks. In particular, we take a well-trained model with its parameters fixed and then we add an adapter based on self-attention with only a few trainable parameters per task to explicitly learn the interaction between an input graph and its retrieved similar graphs. Our experiments on 12 different datasets involving different tasks (classification and regression) show that GraphRetrieval is able to achieve substantial improvements on all twelve datasets compared to three strong GNN baseline models. Our work demonstrates that GraphRetrieval is a promising augmentation for message passing.

Minimal Explanations for Neural Network Predictions

Explaining neural network predictions is known to be a challenging problem. In this paper, we propose a novel approach which can be effectively exploited, either in isolation or in combination with other methods, to enhance the interpretability of neural model predictions. For a given input to a trained neural model, our aim is to compute a smallest set of input features so that the model prediction changes when these features are disregarded by setting them to an uninformative baseline value. While computing such minimal explanations is computationally intractable in general for fully-connected neural networks, we show that the problem becomes solvable in polynomial time by a greedy algorithm under mild assumptions on the network's activation functions. We then show that our tractability result extends seamlessly to more advanced neural architectures such as convolutional and graph neural networks. We conduct experiments to showcase the capability of our method for identifying the input features that are essential to the model's prediction.

MeTeoR: Practical Reasoning in Datalog with Metric Temporal Operators

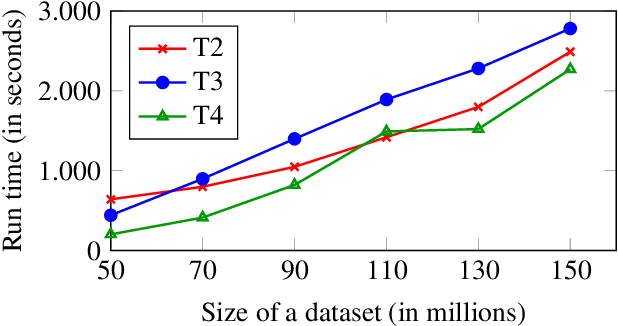
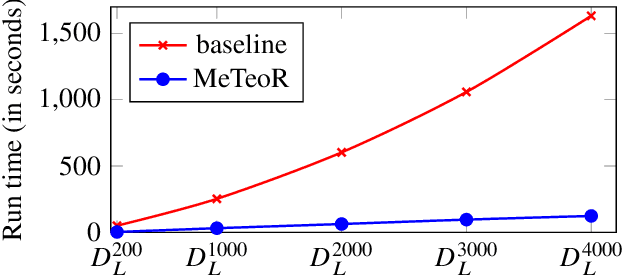
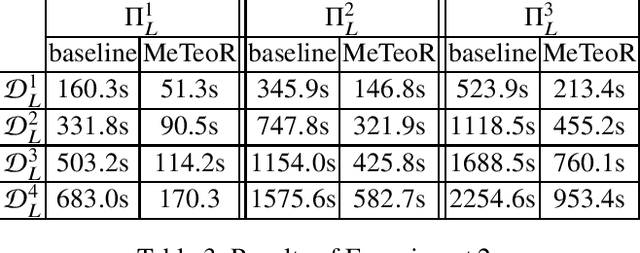
DatalogMTL is an extension of Datalog with operators from metric temporal logic which has received significant attention in recent years. It is a highly expressive knowledge representation language that is well-suited for applications in temporal ontology-based query answering and stream processing. Reasoning in DatalogMTL is, however, of high computational complexity, making implementation challenging and hindering its adoption in applications. In this paper, we present a novel approach for practical reasoning in DatalogMTL which combines materialisation (a.k.a. forward chaining) with automata-based techniques. We have implemented this approach in a reasoner called MeTeoR and evaluated its performance using a temporal extension of the Lehigh University Benchmark and a benchmark based on real-world meteorological data. Our experiments show that MeTeoR is a scalable system which enables reasoning over complex temporal rules and datasets involving tens of millions of temporal facts.

The Window Validity Problem in Rule-Based Stream Reasoning

Rule-based temporal query languages provide the expressive power and flexibility required to capture in a natural way complex analysis tasks over streaming data. Stream processing applications, however, typically require near real-time response using limited resources. In particular, it becomes essential that the underpinning query language has favourable computational properties and that stream processing algorithms are able to keep only a small number of previously received facts in memory at any point in time without sacrificing correctness. In this paper, we propose a recursive fragment of temporal Datalog with tractable data complexity and study the properties of a generic stream reasoning algorithm for this fragment. We focus on the window validity problem as a way to minimise the number of time points for which the stream reasoning algorithm needs to keep data in memory at any point in time.

Consequence-based Reasoning for Description Logics with Disjunction, Inverse Roles, Number Restrictions, and Nominals

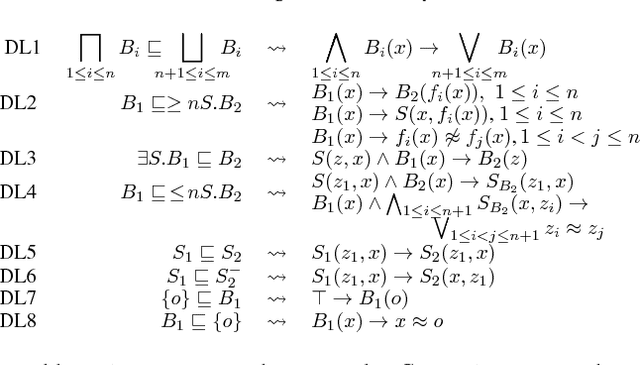
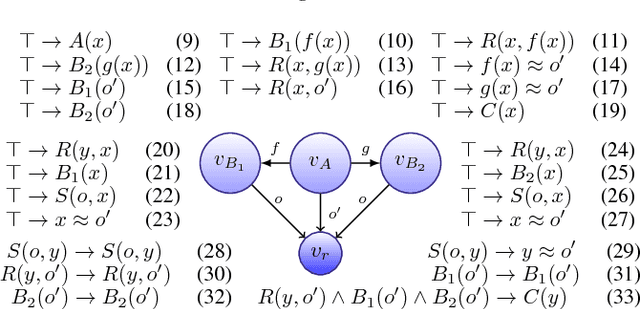
We present a consequence-based calculus for concept subsumption and classification in the description logic ALCHOIQ, which extends ALC with role hierarchies, inverse roles, number restrictions, and nominals. By using standard transformations, our calculus extends to SROIQ, which covers all of OWL 2 DL except for datatypes. A key feature of our calculus is its pay-as-you-go behaviour: unlike existing algorithms, our calculus is worst-case optimal for all the well-known proper fragments of ALCHOIQ, albeit not for the full logic.

Stratified Negation in Limit Datalog Programs

There has recently been an increasing interest in declarative data analysis, where analytic tasks are specified using a logical language, and their implementation and optimisation are delegated to a general-purpose query engine. Existing declarative languages for data analysis can be formalised as variants of logic programming equipped with arithmetic function symbols and/or aggregation, and are typically undecidable. In prior work, the language of $\mathit{limit\ programs}$ was proposed, which is sufficiently powerful to capture many analysis tasks and has decidable entailment problem. Rules in this language, however, do not allow for negation. In this paper, we study an extension of limit programs with stratified negation-as-failure. We show that the additional expressive power makes reasoning computationally more demanding, and provide tight data complexity bounds. We also identify a fragment with tractable data complexity and sufficient expressivity to capture many relevant tasks.