Aggregate-Combine-Readout GNNs Are More Expressive Than Logic C2

In recent years, there has been growing interest in understanding the expressive power of graph neural networks (GNNs) by relating them to logical languages. This research has been been initialised by an influential result of Barcel\'o et al. (2020), who showed that the graded modal logic (or a guarded fragment of the logic C2), characterises the logical expressiveness of aggregate-combine GNNs. As a ``challenging open problem'' they left the question whether full C2 characterises the logical expressiveness of aggregate-combine-readout GNNs. This question has remained unresolved despite several attempts. In this paper, we solve the above open problem by proving that the logical expressiveness of aggregate-combine-readout GNNs strictly exceeds that of C2. This result holds over both undirected and directed graphs. Beyond its implications for GNNs, our work also leads to purely logical insights on the expressive power of infinitary logics.

The Logical Expressiveness of Temporal GNNs via Two-Dimensional Product Logics

In recent years, the expressive power of various neural architectures -- including graph neural networks (GNNs), transformers, and recurrent neural networks -- has been characterised using tools from logic and formal language theory. As the capabilities of basic architectures are becoming well understood, increasing attention is turning to models that combine multiple architectural paradigms. Among them particularly important, and challenging to analyse, are temporal extensions of GNNs, which integrate both spatial (graph-structure) and temporal (evolution over time) dimensions. In this paper, we initiate the study of logical characterisation of temporal GNNs by connecting them to two-dimensional product logics. We show that the expressive power of temporal GNNs depends on how graph and temporal components are combined. In particular, temporal GNNs that apply static GNNs recursively over time can capture all properties definable in the product logic of (past) propositional temporal logic PTL and the modal logic K. In contrast, architectures such as graph-and-time TGNNs and global TGNNs can only express restricted fragments of this logic, where the interaction between temporal and spatial operators is syntactically constrained. These results yield the first logical characterisations of temporal GNNs and establish new relative expressiveness results for temporal GNNs.

Goal-Driven Reasoning in DatalogMTL with Magic Sets

DatalogMTL is a powerful rule-based language for temporal reasoning. Due to its high expressive power and flexible modeling capabilities, it is suitable for a wide range of applications, including tasks from industrial and financial sectors. However, due its high computational complexity, practical reasoning in DatalogMTL is highly challenging. To address this difficulty, we introduce a new reasoning method for DatalogMTL which exploits the magic sets technique -- a rewriting approach developed for (non-temporal) Datalog to simulate top-down evaluation with bottom-up reasoning. We implement this approach and evaluate it on several publicly available benchmarks, showing that the proposed approach significantly and consistently outperforms performance of the state-of-the-art reasoning techniques.

Expressive Power of Temporal Message Passing

Graph neural networks (GNNs) have recently been adapted to temporal settings, often employing temporal versions of the message-passing mechanism known from GNNs. We divide temporal message passing mechanisms from literature into two main types: global and local, and establish Weisfeiler-Leman characterisations for both. This allows us to formally analyse expressive power of temporal message-passing models. We show that global and local temporal message-passing mechanisms have incomparable expressive power when applied to arbitrary temporal graphs. However, the local mechanism is strictly more expressive than the global mechanism when applied to colour-persistent temporal graphs, whose node colours are initially the same in all time points. Our theoretical findings are supported by experimental evidence, underlining practical implications of our analysis.

Seminaive Materialisation in DatalogMTL

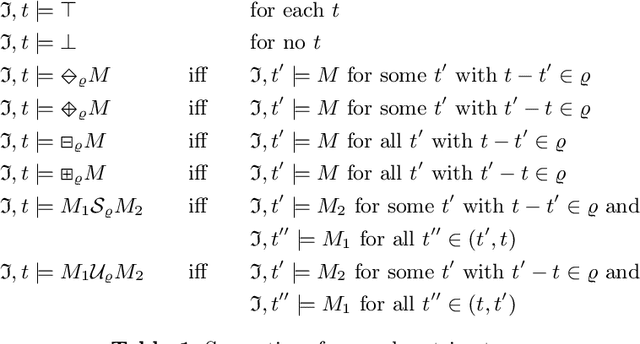
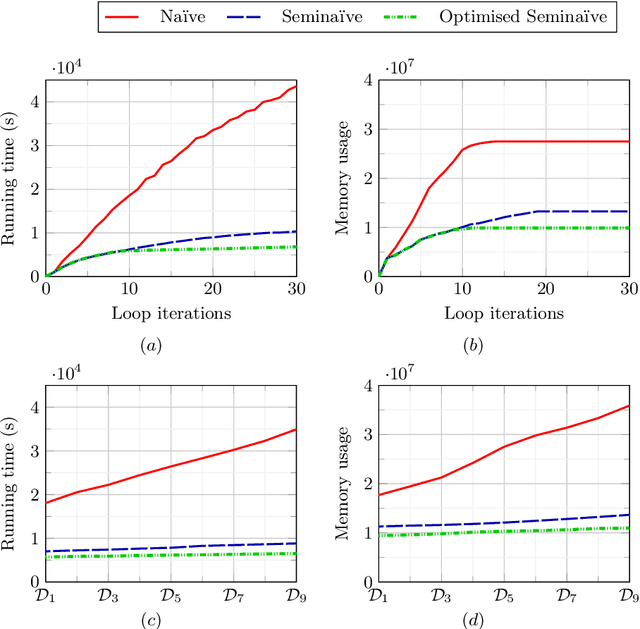
DatalogMTL is an extension of Datalog with metric temporal operators that has found applications in temporal ontology-based data access and query answering, as well as in stream reasoning. Practical algorithms for DatalogMTL are reliant on materialisation-based reasoning, where temporal facts are derived in a forward chaining manner in successive rounds of rule applications. Current materialisation-based procedures are, however, based on a naive evaluation strategy, where the main source of inefficiency stems from redundant computations. In this paper, we propose a materialisation-based procedure which, analogously to the classical seminaive algorithm in Datalog, aims at minimising redundant computation by ensuring that each temporal rule instance is considered at most once during the execution of the algorithm. Our experiments show that our optimised seminaive strategy for DatalogMTL is able to significantly reduce materialisation times.

MeTeoR: Practical Reasoning in Datalog with Metric Temporal Operators

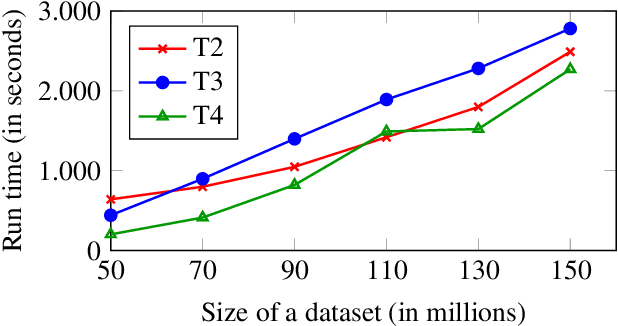
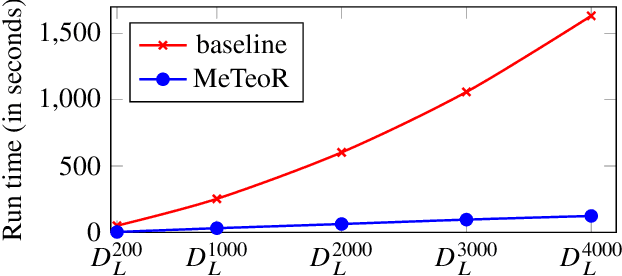
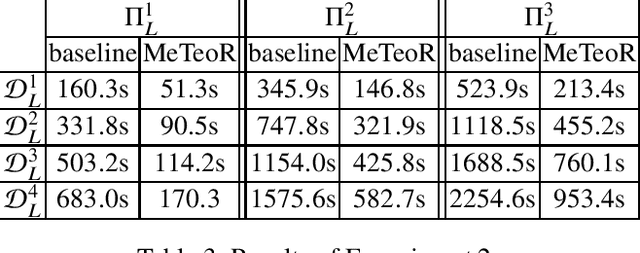
DatalogMTL is an extension of Datalog with operators from metric temporal logic which has received significant attention in recent years. It is a highly expressive knowledge representation language that is well-suited for applications in temporal ontology-based query answering and stream processing. Reasoning in DatalogMTL is, however, of high computational complexity, making implementation challenging and hindering its adoption in applications. In this paper, we present a novel approach for practical reasoning in DatalogMTL which combines materialisation (a.k.a. forward chaining) with automata-based techniques. We have implemented this approach in a reasoner called MeTeoR and evaluated its performance using a temporal extension of the Lehigh University Benchmark and a benchmark based on real-world meteorological data. Our experiments show that MeTeoR is a scalable system which enables reasoning over complex temporal rules and datasets involving tens of millions of temporal facts.

Non-Monotonic Spatial Reasoning with Answer Set Programming Modulo Theories

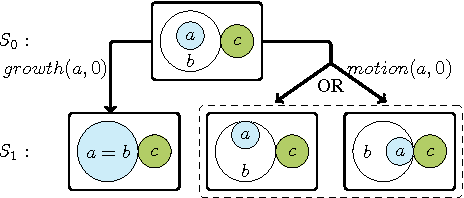
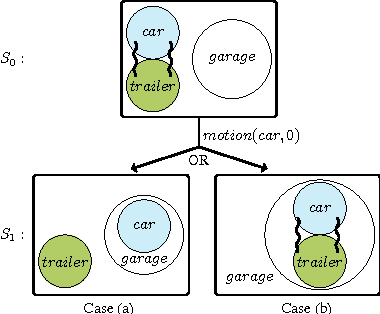
The systematic modelling of dynamic spatial systems is a key requirement in a wide range of application areas such as commonsense cognitive robotics, computer-aided architecture design, and dynamic geographic information systems. We present ASPMT(QS), a novel approach and fully-implemented prototype for non-monotonic spatial reasoning -a crucial requirement within dynamic spatial systems- based on Answer Set Programming Modulo Theories (ASPMT). ASPMT(QS) consists of a (qualitative) spatial representation module (QS) and a method for turning tight ASPMT instances into Satisfiability Modulo Theories (SMT) instances in order to compute stable models by means of SMT solvers. We formalise and implement concepts of default spatial reasoning and spatial frame axioms. Spatial reasoning is performed by encoding spatial relations as systems of polynomial constraints, and solving via SMT with the theory of real nonlinear arithmetic. We empirically evaluate ASPMT(QS) in comparison with other contemporary spatial reasoning systems both within and outside the context of logic programming. ASPMT(QS) is currently the only existing system that is capable of reasoning about indirect spatial effects (i.e., addressing the ramification problem), and integrating geometric and qualitative spatial information within a non-monotonic spatial reasoning context. This paper is under consideration for publication in TPLP.

ASPMT(QS): Non-Monotonic Spatial Reasoning with Answer Set Programming Modulo Theories

The systematic modelling of \emph{dynamic spatial systems} [9] is a key requirement in a wide range of application areas such as comonsense cognitive robotics, computer-aided architecture design, dynamic geographic information systems. We present ASPMT(QS), a novel approach and fully-implemented prototype for non-monotonic spatial reasoning ---a crucial requirement within dynamic spatial systems-- based on Answer Set Programming Modulo Theories (ASPMT). ASPMT(QS) consists of a (qualitative) spatial representation module (QS) and a method for turning tight ASPMT instances into Sat Modulo Theories (SMT) instances in order to compute stable models by means of SMT solvers. We formalise and implement concepts of default spatial reasoning and spatial frame axioms using choice formulas. Spatial reasoning is performed by encoding spatial relations as systems of polynomial constraints, and solving via SMT with the theory of real nonlinear arithmetic. We empirically evaluate ASPMT(QS) in comparison with other prominent contemporary spatial reasoning systems. Our results show that ASPMT(QS) is the only existing system that is capable of reasoning about indirect spatial effects (i.e. addressing the ramification problem), and integrating geometric and qualitative spatial information within a non-monotonic spatial reasoning context.