The Computational Complexity of Formal Reasoning for Encoder-Only Transformers

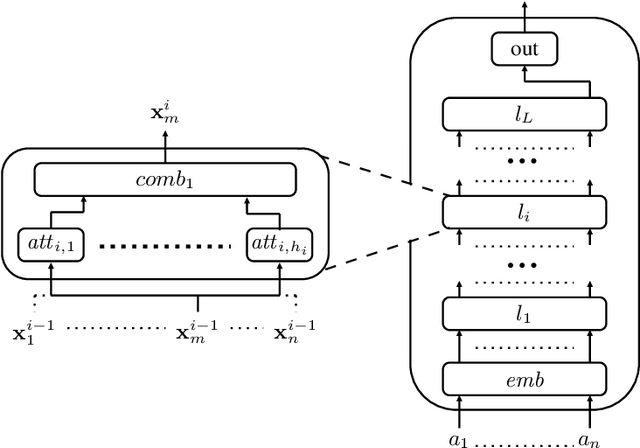
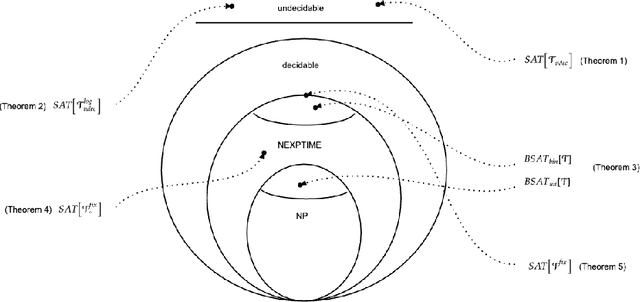
We investigate challenges and possibilities of formal reasoning for encoder-only transformers (EOT), meaning sound and complete methods for verifying or interpreting behaviour. In detail, we condense related formal reasoning tasks in the form of a naturally occurring satisfiability problem (SAT). We find that SAT is undecidable if we consider EOT, commonly considered in the expressiveness community. Furthermore, we identify practical scenarios where SAT is decidable and establish corresponding complexity bounds. Besides trivial cases, we find that quantized EOT, namely those restricted by some fixed-width arithmetic, lead to the decidability of SAT due to their limited attention capabilities. However, the problem remains difficult, as we establish those scenarios where SAT is NEXPTIME-hard and those where we can show that it is solvable in NEXPTIME for quantized EOT. To complement our theoretical results, we put our findings and their implications in the overall perspective of formal reasoning.

Verifying And Interpreting Neural Networks using Finite Automata

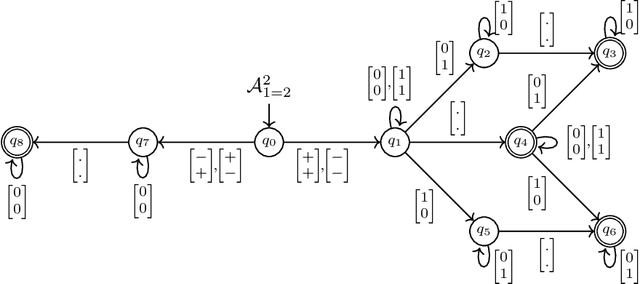
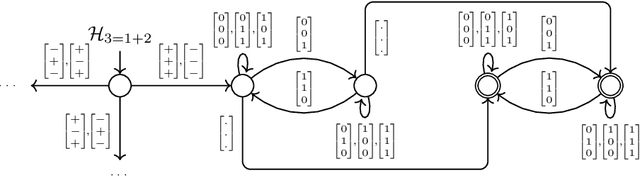
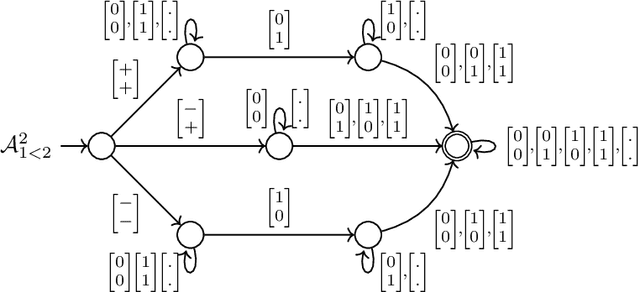
Verifying properties and interpreting the behaviour of deep neural networks (DNN) is an important task given their ubiquitous use in applications, including safety-critical ones, and their blackbox nature. We propose an automata-theoric approach to tackling problems arising in DNN analysis. We show that the input-output behaviour of a DNN can be captured precisely by a (special) weak B\"uchi automaton of exponential size. We show how these can be used to address common verification and interpretation tasks like adversarial robustness, minimum sufficient reasons etc. We report on a proof-of-concept implementation translating DNN to automata on finite words for better efficiency at the cost of losing precision in analysis.

We Cannot Guarantee Safety: The Undecidability of Graph Neural Network Verification

Graph Neural Networks (GNN) are commonly used for two tasks: (whole) graph classification and node classification. We formally introduce generically formulated decision problems for both tasks, corresponding to the following pattern: given a GNN, some specification of valid inputs, and some specification of valid outputs, decide whether there is a valid input satisfying the output specification. We then prove that graph classifier verification is undecidable in general, implying that there cannot be an algorithm surely guaranteeing the absence of misclassification of any kind. Additionally, we show that verification in the node classification case becomes decidable as soon as we restrict the degree of the considered graphs. Furthermore, we discuss possible changes to these results depending on the considered GNN model and specifications.

Reachability In Simple Neural Networks

We investigate the complexity of the reachability problem for (deep) neural networks: does it compute valid output given some valid input? It was recently claimed that the problem is NP-complete for general neural networks and specifications over the input/output dimension given by conjunctions of linear inequalities. We recapitulate the proof and repair some flaws in the original upper and lower bound proofs. Motivated by the general result, we show that NP-hardness already holds for restricted classes of simple specifications and neural networks. Allowing for a single hidden layer and an output dimension of one as well as neural networks with just one negative, zero and one positive weight or bias is sufficient to ensure NP-hardness. Additionally, we give a thorough discussion and outlook of possible extensions for this direction of research on neural network verification.

Reachability Is NP-Complete Even for the Simplest Neural Networks

We investigate the complexity of the reachability problem for (deep) neural networks: does it compute valid output given some valid input? It was recently claimed that the problem is NP-complete for general neural networks and conjunctive input/output specifications. We repair some flaws in the original upper and lower bound proofs. We then show that NP-hardness already holds for restricted classes of simple specifications and neural networks with just one layer, as well as neural networks with minimal requirements on the occurring parameters.