The Computational Complexity of Formal Reasoning for Encoder-Only Transformers
Paper and Code
May 28, 2024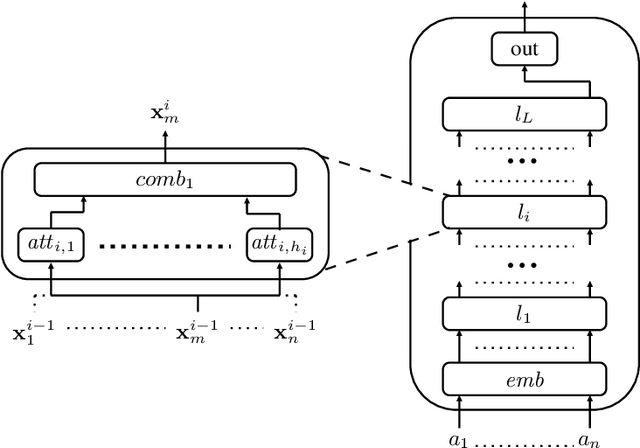
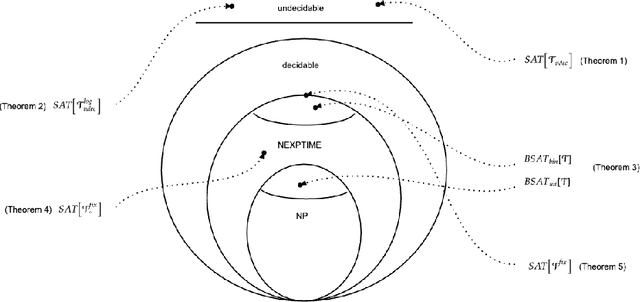
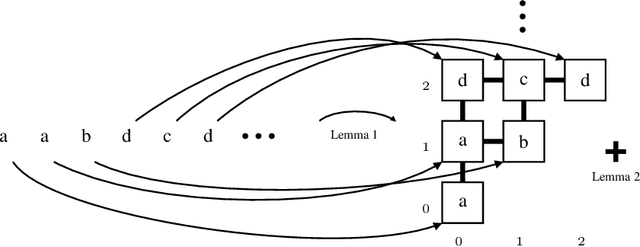
We investigate challenges and possibilities of formal reasoning for encoder-only transformers (EOT), meaning sound and complete methods for verifying or interpreting behaviour. In detail, we condense related formal reasoning tasks in the form of a naturally occurring satisfiability problem (SAT). We find that SAT is undecidable if we consider EOT, commonly considered in the expressiveness community. Furthermore, we identify practical scenarios where SAT is decidable and establish corresponding complexity bounds. Besides trivial cases, we find that quantized EOT, namely those restricted by some fixed-width arithmetic, lead to the decidability of SAT due to their limited attention capabilities. However, the problem remains difficult, as we establish those scenarios where SAT is NEXPTIME-hard and those where we can show that it is solvable in NEXPTIME for quantized EOT. To complement our theoretical results, we put our findings and their implications in the overall perspective of formal reasoning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge