On the Expressiveness of State Space Models via Temporal Logics

We investigate the expressive power of state space models (SSM), which have recently emerged as a potential alternative to transformer architectures in large language models. Building on recent work, we analyse SSM expressiveness through fragments and extensions of linear temporal logic over finite traces. Our results show that the expressive capabilities of SSM vary substantially depending on the underlying gating mechanism. We further distinguish between SSM operating over fixed-width arithmetic (quantised models), whose expressive power remains within regular languages, and SSM with unbounded precision, which can capture counting properties and non-regular languages. In addition, we provide a systematic comparison between these different SSM variants and known results on transformers, thereby clarifying how the two architectures relate in terms of expressive power.

The Computational Complexity of Satisfiability in State Space Models

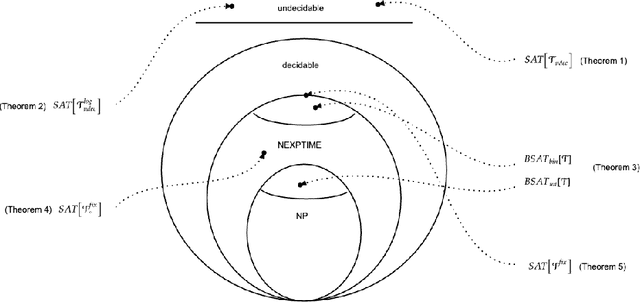
We analyse the complexity of the satisfiability problem ssmSAT for State Space Models (SSM), which asks whether an input sequence can lead the model to an accepting configuration. We find that ssmSAT is undecidable in general, reflecting the computational power of SSM. Motivated by practical settings, we identify two natural restrictions under which ssmSAT becomes decidable and establish corresponding complexity bounds. First, for SSM with bounded context length, ssmSAT is NP-complete when the input length is given in unary and in NEXPTIME (and PSPACE-hard) when the input length is given in binary. Second, for quantised SSM operating over fixed-width arithmetic, ssmSAT is PSPACE-complete resp. in EXPSPACE depending on the bit-width encoding. While these results hold for diagonal gated SSM we also establish complexity bounds for time-invariant SSM. Our results establish a first complexity landscape for formal reasoning in SSM and highlight fundamental limits and opportunities for the verification of SSM-based language models.

The Computational Complexity of Formal Reasoning for Encoder-Only Transformers

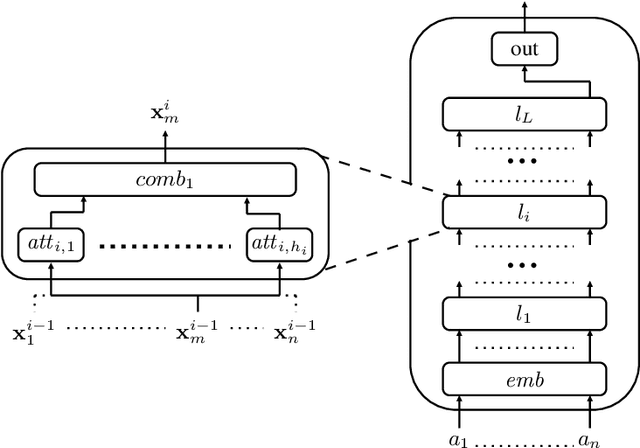
We investigate challenges and possibilities of formal reasoning for encoder-only transformers (EOT), meaning sound and complete methods for verifying or interpreting behaviour. In detail, we condense related formal reasoning tasks in the form of a naturally occurring satisfiability problem (SAT). We find that SAT is undecidable if we consider EOT, commonly considered in the expressiveness community. Furthermore, we identify practical scenarios where SAT is decidable and establish corresponding complexity bounds. Besides trivial cases, we find that quantized EOT, namely those restricted by some fixed-width arithmetic, lead to the decidability of SAT due to their limited attention capabilities. However, the problem remains difficult, as we establish those scenarios where SAT is NEXPTIME-hard and those where we can show that it is solvable in NEXPTIME for quantized EOT. To complement our theoretical results, we put our findings and their implications in the overall perspective of formal reasoning.

Verifying And Interpreting Neural Networks using Finite Automata

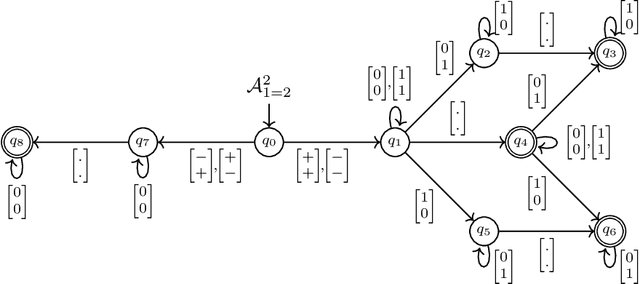
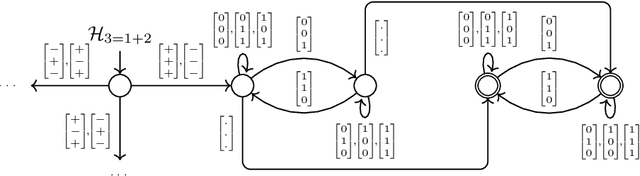
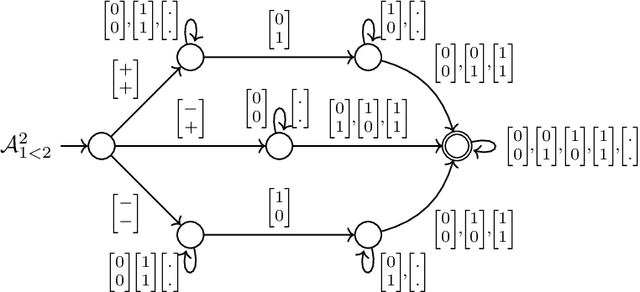
Verifying properties and interpreting the behaviour of deep neural networks (DNN) is an important task given their ubiquitous use in applications, including safety-critical ones, and their blackbox nature. We propose an automata-theoric approach to tackling problems arising in DNN analysis. We show that the input-output behaviour of a DNN can be captured precisely by a (special) weak B\"uchi automaton of exponential size. We show how these can be used to address common verification and interpretation tasks like adversarial robustness, minimum sufficient reasons etc. We report on a proof-of-concept implementation translating DNN to automata on finite words for better efficiency at the cost of losing precision in analysis.