Expressive Power of Temporal Message Passing

Graph neural networks (GNNs) have recently been adapted to temporal settings, often employing temporal versions of the message-passing mechanism known from GNNs. We divide temporal message passing mechanisms from literature into two main types: global and local, and establish Weisfeiler-Leman characterisations for both. This allows us to formally analyse expressive power of temporal message-passing models. We show that global and local temporal message-passing mechanisms have incomparable expressive power when applied to arbitrary temporal graphs. However, the local mechanism is strictly more expressive than the global mechanism when applied to colour-persistent temporal graphs, whose node colours are initially the same in all time points. Our theoretical findings are supported by experimental evidence, underlining practical implications of our analysis.

Superposition with Delayed Unification

Classically, in saturation-based proof systems, unification has been considered atomic. However, it is also possible to move unification to the calculus level, turning the steps of the unification algorithm into inferences. For calculi that rely on unification procedures returning large or even infinite sets of unifiers, integrating unification into the calculus is an attractive method of dovetailing unification and inference. This applies, for example, to AC-superposition and higher-order superposition. We show that first-order superposition remains complete when moving unification rules to the calculus level. We discuss some of the benefits this has even for standard first-order superposition and provide an experimental evaluation.

Lemmas: Generation, Selection, Application

Noting that lemmas are a key feature of mathematics, we engage in an investigation of the role of lemmas in automated theorem proving. The paper describes experiments with a combined system involving learning technology that generates useful lemmas for automated theorem provers, demonstrating improvement for several representative systems and solving a hard problem not solved by any system for twenty years. By focusing on condensed detachment problems we simplify the setting considerably, allowing us to get at the essence of lemmas and their role in proof search.

Topological Data Analysis for Word Sense Disambiguation

We develop and test a novel unsupervised algorithm for word sense induction and disambiguation which uses topological data analysis. Typical approaches to the problem involve clustering, based on simple low level features of distance in word embeddings. Our approach relies on advanced mathematical concepts in the field of topology which provides a richer conceptualization of clusters for the word sense induction tasks. We use a persistent homology barcode algorithm on the SemCor dataset and demonstrate that our approach gives low relative error on word sense induction. This shows the promise of topological algorithms for natural language processing and we advocate for future work in this promising area.

Optimal Transport for Super Resolution Applied to Astronomy Imaging

Super resolution is an essential tool in optics, especially on interstellar scales, due to physical laws restricting possible imaging resolution. We propose using optimal transport and entropy for super resolution applications. We prove that the reconstruction is accurate when sparsity is known and noise or distortion is small enough. We prove that the optimizer is stable and robust to noise and perturbations. We compare this method to a state of the art convolutional neural network and get similar results for much less computational cost and greater methodological flexibility.

Top-K Ranking Deep Contextual Bandits for Information Selection Systems

In today's technology environment, information is abundant, dynamic, and heterogeneous in nature. Automated filtering and prioritization of information is based on the distinction between whether the information adds substantial value toward one's goal or not. Contextual multi-armed bandit has been widely used for learning to filter contents and prioritize according to user interest or relevance. Learn-to-Rank technique optimizes the relevance ranking on items, allowing the contents to be selected accordingly. We propose a novel approach to top-K rankings under the contextual multi-armed bandit framework. We model the stochastic reward function with a neural network to allow non-linear approximation to learn the relationship between rewards and contexts. We demonstrate the approach and evaluate the the performance of learning from the experiments using real world data sets in simulated scenarios. Empirical results show that this approach performs well under the complexity of a reward structure and high dimensional contextual features.

Convergence Guarantees for Deep Epsilon Greedy Policy Learning

Policy learning is a quickly growing area. As robotics and computers control day-to-day life, their error rate needs to be minimized and controlled. There are many policy learning methods and provable error rates that accompany them. We show an error or regret bound and convergence of the Deep Epsilon Greedy method which chooses actions with a neural network's prediction. In experiments with the real-world dataset MNIST, we construct a nonlinear reinforcement learning problem. We witness how with either high or low noise, some methods do and some do not converge which agrees with our proof of convergence.

Deep Upper Confidence Bound Algorithm for Contextual Bandit Ranking of Information Selection

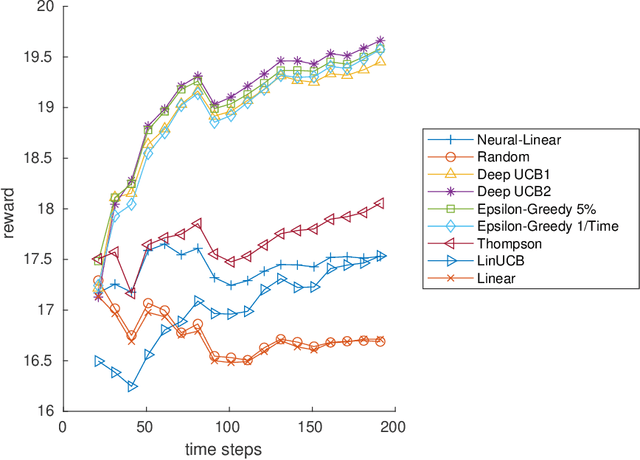
Contextual multi-armed bandits (CMAB) have been widely used for learning to filter and prioritize information according to a user's interest. In this work, we analyze top-K ranking under the CMAB framework where the top-K arms are chosen iteratively to maximize a reward. The context, which represents a set of observable factors related to the user, is used to increase prediction accuracy compared to a standard multi-armed bandit. Contextual bandit methods have mostly been studied under strict linearity assumptions, but we drop that assumption and learn non-linear stochastic reward functions with deep neural networks. We introduce a novel algorithm called the Deep Upper Confidence Bound (UCB) algorithm. Deep UCB balances exploration and exploitation with a separate neural network to model the learning convergence. We compare the performance of many bandit algorithms varying K over real-world data sets with high-dimensional data and non-linear reward functions. Empirical results show that the performance of Deep UCB often outperforms though it is sensitive to the problem and reward setup. Additionally, we prove theoretical regret bounds on Deep UCB giving convergence to optimality for the weak class of CMAB problems.